REBEL: Hidden Knowledge Recovery via Evolutionary-Based Evaluation Loop

Machine unlearning for LLMs aims to remove sensitive or copyrighted data from trained models. However, the true efficacy of current unlearning methods remains uncertain. Standard evaluation metrics rely on benign queries that often mistake superficial information suppression for genuine knowledge removal. Such metrics fail to detect residual knowledge that more sophisticated prompting strategies could still extract. We introduce REBEL, an evolutionary approach for adversarial prompt generation designed to probe whether unlearned data can still be recovered. Our experiments demonstrate that REBEL successfully elicits ``forgotten'' knowledge from models that seemed to be forgotten in standard unlearning benchmarks, revealing that current unlearning methods may provide only a superficial layer of protection. We validate our framework on subsets of the TOFU and WMDP benchmarks, evaluating performance across a diverse suite of unlearning algorithms. Our experiments show that REBEL consistently outperforms static baselines, recovering ``forgotten'' knowledge with Attack Success Rates (ASRs) reaching up to 60% on TOFU and 93% on WMDP. We will make all code publicly available upon acceptance. Code is available at https://github.com/patryk-rybak/REBEL/

QuantumGS: Quantum Encoding Framework for Gaussian Splatting

Recent advances in neural rendering, particularly 3D Gaussian Splatting (3DGS), have enabled real-time rendering of complex scenes. However, standard 3DGS relies on spherical harmonics, which often struggle to accurately capture high-frequency view-dependent effects such as sharp reflections and transparency. While hybrid approaches like Viewing Direction Gaussian Splatting (VDGS) mitigate this limitation using classical Multi-Layer Perceptrons (MLPs), they remain limited by the expressivity of classical networks in low-parameter regimes. In this paper, we introduce QuantumGS, a novel hybrid framework that integrates Variational Quantum Circuits (VQC) into the Gaussian Splatting pipeline. We propose a unique encoding strategy that maps the viewing direction directly onto the Bloch sphere, leveraging the natural geometry of qubits to represent 3D directional data. By replacing classical color-modulating networks with quantum circuits generated via a hypernetwork or conditioning mechanism, we achieve higher expressivity and better generalization. Source code is available in the supplementary material. Code is available at https://github.com/gwilczynski95/QuantumGS

AnyStyle: Single-Pass Multimodal Stylization for 3D Gaussian Splatting

The growing demand for rapid and scalable 3D asset creation has driven interest in feed-forward 3D reconstruction methods, with 3D Gaussian Splatting (3DGS) emerging as an effective scene representation. While recent approaches have demonstrated pose-free reconstruction from unposed image collections, integrating stylization or appearance control into such pipelines remains underexplored. Existing attempts largely rely on image-based conditioning, which limits both controllability and flexibility. In this work, we introduce AnyStyle, a feed-forward 3D reconstruction and stylization framework that enables pose-free, zero-shot stylization through multimodal conditioning. Our method supports both textual and visual style inputs, allowing users to control the scene appearance using natural language descriptions or reference images. We propose a modular stylization architecture that requires only minimal architectural modifications and can be integrated into existing feed-forward 3D reconstruction backbones. Experiments demonstrate that AnyStyle improves style controllability over prior feed-forward stylization methods while preserving high-quality geometric reconstruction. A user study further confirms that AnyStyle achieves superior stylization quality compared to an existing state-of-the-art approach. Repository: https://github.com/joaxkal/AnyStyle.

UnHype: CLIP-Guided Hypernetworks for Dynamic LoRA Unlearning

Recent advances in large-scale diffusion models have intensified concerns about their potential misuse, particularly in generating realistic yet harmful or socially disruptive content. This challenge has spurred growing interest in effective machine unlearning, the process of selectively removing specific knowledge or concepts from a model without compromising its overall generative capabilities. Among various approaches, Low-Rank Adaptation (LoRA) has emerged as an effective and efficient method for fine-tuning models toward targeted unlearning. However, LoRA-based methods often exhibit limited adaptability to concept semantics and struggle to balance removing closely related concepts with maintaining generalization across broader meanings. Moreover, these methods face scalability challenges when multiple concepts must be erased simultaneously. To address these limitations, we introduce UnHype, a framework that incorporates hypernetworks into single- and multi-concept LoRA training. The proposed architecture can be directly plugged into Stable Diffusion as well as modern flow-based text-to-image models, where it demonstrates stable training behavior and effective concept control. During inference, the hypernetwork dynamically generates adaptive LoRA weights based on the CLIP embedding, enabling more context-aware, scalable unlearning. We evaluate UnHype across several challenging tasks, including object erasure, celebrity erasure, and explicit content removal, demonstrating its effectiveness and versatility. Repository: https://github.com/gmum/UnHype.

DIAMOND: Directed Inference for Artifact Mitigation in Flow Matching Models

Despite impressive results from recent text-to-image models like FLUX, visual and anatomical artifacts remain a significant hurdle for practical and professional use. Existing methods for artifact reduction, typically work in a post-hoc manner, consequently failing to intervene effectively during the core image formation process. Notably, current techniques require problematic and invasive modifications to the model weights, or depend on a computationally expensive and time-consuming process of regional refinement. To address these limitations, we propose DIAMOND, a training-free method that applies trajectory correction to mitigate artifacts during inference. By reconstructing an estimate of the clean sample at every step of the generative trajectory, DIAMOND actively steers the generation process away from latent states that lead to artifacts. Furthermore, we extend the proposed method to standard Diffusion Models, demonstrating that DIAMOND provides a robust, zero-shot path to high-fidelity, artifact-free image synthesis without the need for additional training or weight modifications in modern generative architectures. Code is available at https://gmum.github.io/DIAMOND/

ReLAPSe: Reinforcement-Learning-trained Adversarial Prompt Search for Erased concepts in unlearned diffusion models

Machine unlearning is a key defense mechanism for removing unauthorized concepts from text-to-image diffusion models, yet recent evidence shows that latent visual information often persists after unlearning. Existing adversarial approaches for exploiting this leakage are constrained by fundamental limitations: optimization-based methods are computationally expensive due to per-instance iterative search. At the same time, reasoning-based and heuristic techniques lack direct feedback from the target model's latent visual representations. To address these challenges, we introduce ReLAPSe, a policy-based adversarial framework that reformulates concept restoration as a reinforcement learning problem. ReLAPSe trains an agent using Reinforcement Learning with Verifiable Rewards (RLVR), leveraging the diffusion model's noise prediction loss as a model-intrinsic and verifiable feedback signal. This closed-loop design directly aligns textual prompt manipulation with latent visual residuals, enabling the agent to learn transferable restoration strategies rather than optimizing isolated prompts. By pioneering the shift from per-instance optimization to global policy learning, ReLAPSe achieves efficient, near-real-time recovery of fine-grained identities and styles across multiple state-of-the-art unlearning methods, providing a scalable tool for rigorous red-teaming of unlearned diffusion models. Some experimental evaluations involve sensitive visual concepts, such as nudity. Code is available at https://github.com/gmum/ReLaPSe

From Unlearning to UNBRANDING: A Benchmark for Trademark-Safe Text-to-Image Generation

The rapid progress of text-to-image diffusion models raises significant concerns regarding the unauthorized reproduction of trademarked content. While prior work targets general concepts (e.g., styles, celebrities), it fails to address specific brand identifiers. Crucially, we note that brand recognition is multi-dimensional, extending beyond explicit logos to encompass distinctive structural features (e.g., a car's front grille). To tackle this, we introduce unbranding, a novel task for the fine-grained removal of both trademarks and subtle structural brand features, while preserving semantic coherence. To facilitate research, we construct a comprehensive benchmark dataset. Recognizing that existing brand detectors are limited to logos and fail to capture abstract trade dress (e.g., the shape of a Coca-Cola bottle), we introduce a novel evaluation metric based on Vision Language Models (VLMs). This VLM-based metric uses a question-answering framework to probe images for both explicit logos and implicit, holistic brand characteristics. Furthermore, we observe that as model fidelity increases, with newer systems (SDXL, FLUX) synthesizing brand identifiers more readily than older models (Stable Diffusion), the urgency of the unbranding challenge is starkly highlighted. Our results, validated by our VLM metric, confirm unbranding is a distinct, practically relevant problem requiring specialized techniques. Project Page: https://gmum.github.io/UNBRANDING/.

SHIELD: Secure Hypernetworks for Incremental Expansion Learning Defense

Traditional deep neural networks suffer from several limitations, including catastrophic forgetting. When models are adapted to new datasets, they tend to quickly forget previously learned knowledge. Another significant issue is the lack of robustness to even small perturbations in the input data. In practice, we can often easily perform adversarial attacks and change the network's predictions, adding minimal noise to the input. Dedicated architectures and training procedures can solve each of the above problems separately. Unfortunately, currently, no model can simultaneously address both catastrophic forgetting and vulnerability to adversarial attacks. We introduce SHIELD (Secure Hypernetworks for Incremental Expansion and Learning Defense), a novel approach that integrates a hypernetwork-based continual learning approach with interval arithmetic. SHIELD use the hypernetwork to transfer trainable task embedding vectors into the weights of a target model dedicated to specific data. This paradigm allows for the dynamic generation of separate networks for each subtask, while the hypernetwork aggregates and analyzes information across all tasks. The target model takes in the input a data sample with a defined interval range, and by creating a hypercube, produces a prediction for the given range. Therefore, such target models provide strict guarantees against all possible attacks for data samples within the interval range. Our approach enhances security without sacrificing network adaptability, addressing the overlooked challenge of safety in continual learning.

HuSc3D: Human Sculpture dataset for 3D object reconstruction

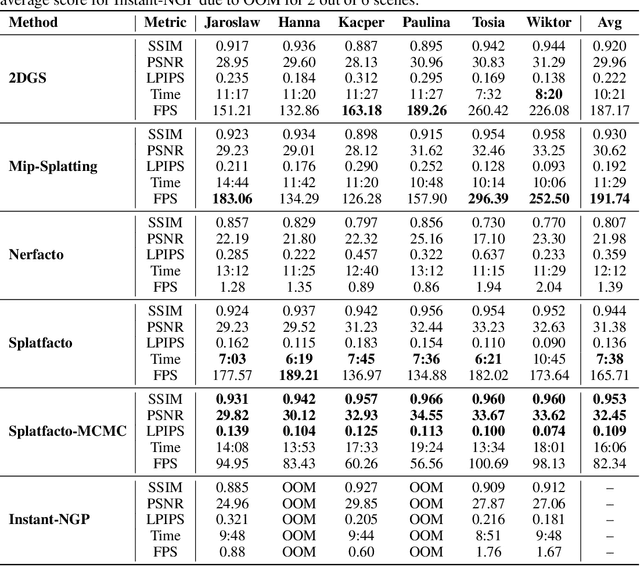
3D scene reconstruction from 2D images is one of the most important tasks in computer graphics. Unfortunately, existing datasets and benchmarks concentrate on idealized synthetic or meticulously captured realistic data. Such benchmarks fail to convey the inherent complexities encountered in newly acquired real-world scenes. In such scenes especially those acquired outside, the background is often dynamic, and by popular usage of cell phone cameras, there might be discrepancies in, e.g., white balance. To address this gap, we present HuSc3D, a novel dataset specifically designed for rigorous benchmarking of 3D reconstruction models under realistic acquisition challenges. Our dataset uniquely features six highly detailed, fully white sculptures characterized by intricate perforations and minimal textural and color variation. Furthermore, the number of images per scene varies significantly, introducing the additional challenge of limited training data for some instances alongside scenes with a standard number of views. By evaluating popular 3D reconstruction methods on this diverse dataset, we demonstrate the distinctiveness of HuSc3D in effectively differentiating model performance, particularly highlighting the sensitivity of methods to fine geometric details, color ambiguity, and varying data availability--limitations often masked by more conventional datasets.

CLIPGaussian: Universal and Multimodal Style Transfer Based on Gaussian Splatting

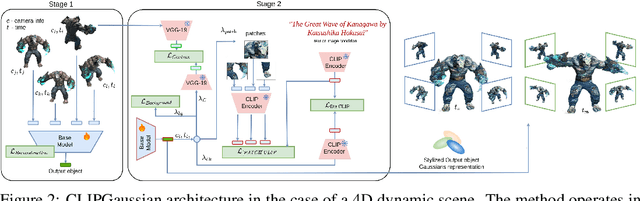
Gaussian Splatting (GS) has recently emerged as an efficient representation for rendering 3D scenes from 2D images and has been extended to images, videos, and dynamic 4D content. However, applying style transfer to GS-based representations, especially beyond simple color changes, remains challenging. In this work, we introduce CLIPGaussians, the first unified style transfer framework that supports text- and image-guided stylization across multiple modalities: 2D images, videos, 3D objects, and 4D scenes. Our method operates directly on Gaussian primitives and integrates into existing GS pipelines as a plug-in module, without requiring large generative models or retraining from scratch. CLIPGaussians approach enables joint optimization of color and geometry in 3D and 4D settings, and achieves temporal coherence in videos, while preserving a model size. We demonstrate superior style fidelity and consistency across all tasks, validating CLIPGaussians as a universal and efficient solution for multimodal style transfer.