MeshSplats: Mesh-Based Rendering with Gaussian Splatting Initialization

Gaussian Splatting (GS) is a recent and pivotal technique in 3D computer graphics. GS-based algorithms almost always bypass classical methods such as ray tracing, which offers numerous inherent advantages for rendering. For example, ray tracing is able to handle incoherent rays for advanced lighting effects, including shadows and reflections. To address this limitation, we introduce MeshSplats, a method which converts GS to a mesh-like format. Following the completion of training, MeshSplats transforms Gaussian elements into mesh faces, enabling rendering using ray tracing methods with all their associated benefits. Our model can be utilized immediately following transformation, yielding a mesh of slightly reduced quality without additional training. Furthermore, we can enhance the reconstruction quality through the application of a dedicated optimization algorithm that operates on mesh faces rather than Gaussian components. The efficacy of our method is substantiated by experimental results, underscoring its extensive applications in computer graphics and image processing.

Tight Bounds on Jensen's Gap: Novel Approach with Applications in Generative Modeling

Among various mathematical tools of particular interest are those that provide a common basis for researchers in different scientific fields. One of them is Jensen's inequality, which states that the expectation of a convex function is greater than or equal to the function evaluated at the expectation. The resulting difference, known as Jensen's gap, became the subject of investigation by both the statistical and machine learning communities. Among many related topics, finding lower and upper bounds on Jensen's gap (under different assumptions on the underlying function and distribution) has recently become a problem of particular interest. In our paper, we take another step in this direction by providing a novel general and mathematically rigorous technique, motivated by the recent results of Struski et al. (2023). In addition, by studying in detail the case of the logarithmic function and the log-normal distribution, we explore a method for tightly estimating the log-likelihood of generative models trained on real-world datasets. Furthermore, we present both analytical and experimental arguments in support of the superiority of our approach in comparison to existing state-of-the-art solutions, contingent upon fulfillment of the criteria set forth by theoretical studies and corresponding experiments on synthetic data.

RaySplats: Ray Tracing based Gaussian Splatting

3D Gaussian Splatting (3DGS) is a process that enables the direct creation of 3D objects from 2D images. This representation offers numerous advantages, including rapid training and rendering. However, a significant limitation of 3DGS is the challenge of incorporating light and shadow reflections, primarily due to the utilization of rasterization rather than ray tracing for rendering. This paper introduces RaySplats, a model that employs ray-tracing based Gaussian Splatting. Rather than utilizing the projection of Gaussians, our method employs a ray-tracing mechanism, operating directly on Gaussian primitives represented by confidence ellipses with RGB colors. In practice, we compute the intersection between ellipses and rays to construct ray-tracing algorithms, facilitating the incorporation of meshes with Gaussian Splatting models and the addition of lights, shadows, and other related effects.

VeGaS: Video Gaussian Splatting

Implicit Neural Representations (INRs) employ neural networks to approximate discrete data as continuous functions. In the context of video data, such models can be utilized to transform the coordinates of pixel locations along with frame occurrence times (or indices) into RGB color values. Although INRs facilitate effective compression, they are unsuitable for editing purposes. One potential solution is to use a 3D Gaussian Splatting (3DGS) based model, such as the Video Gaussian Representation (VGR), which is capable of encoding video as a multitude of 3D Gaussians and is applicable for numerous video processing operations, including editing. Nevertheless, in this case, the capacity for modification is constrained to a limited set of basic transformations. To address this issue, we introduce the Video Gaussian Splatting (VeGaS) model, which enables realistic modifications of video data. To construct VeGaS, we propose a novel family of Folded-Gaussian distributions designed to capture nonlinear dynamics in a video stream and model consecutive frames by 2D Gaussians obtained as respective conditional distributions. Our experiments demonstrate that VeGaS outperforms state-of-the-art solutions in frame reconstruction tasks and allows realistic modifications of video data. The code is available at: https://github.com/gmum/VeGaS.

GASP: Gaussian Splatting for Physic-Based Simulations

Physics simulation is paramount for modeling and utilization of 3D scenes in various real-world applications. However, its integration with state-of-the-art 3D scene rendering techniques such as Gaussian Splatting (GS) remains challenging. Existing models use additional meshing mechanisms, including triangle or tetrahedron meshing, marching cubes, or cage meshes. As an alternative, we can modify the physics grounded Newtonian dynamics to align with 3D Gaussian components. Current models take the first-order approximation of a deformation map, which locally approximates the dynamics by linear transformations. In contrast, our Gaussian Splatting for Physics-Based Simulations (GASP) model uses such a map (without any modifications) and flat Gaussian distributions, which are parameterized by three points (mesh faces). Subsequently, each 3D point (mesh face node) is treated as a discrete entity within a 3D space. Consequently, the problem of modeling Gaussian components is reduced to working with 3D points. Additionally, the information on mesh faces can be used to incorporate further properties into the physics model, facilitating the use of triangles. Resulting solution can be integrated into any physics engine that can be treated as a black box. As demonstrated in our studies, the proposed model exhibits superior performance on a diverse range of benchmark datasets designed for 3D object rendering.

PrAViC: Probabilistic Adaptation Framework for Real-Time Video Classification

Video processing is generally divided into two main categories: processing of the entire video, which typically yields optimal classification outcomes, and real-time processing, where the objective is to make a decision as promptly as possible. The latter is often driven by the need to identify rapidly potential critical or dangerous situations. These could include machine failure, traffic accidents, heart problems, or dangerous behavior. Although the models dedicated to the processing of entire videos are typically well-defined and clearly presented in the literature, this is not the case for online processing, where a plethora of hand-devised methods exist. To address this, we present \our{}, a novel, unified, and theoretically-based adaptation framework for dealing with the online classification problem for video data. The initial phase of our study is to establish a robust mathematical foundation for the theory of classification of sequential data, with the potential to make a decision at an early stage. This allows us to construct a natural function that encourages the model to return an outcome much faster. The subsequent phase is to demonstrate a straightforward and readily implementable method for adapting offline models to online and recurrent operations. Finally, by comparing the proposed approach to the non-online state-of-the-art baseline, it is demonstrated that the use of \our{} encourages the network to make earlier classification decisions without compromising accuracy.

HyperPlanes: Hypernetwork Approach to Rapid NeRF Adaptation

Neural radiance fields (NeRFs) are a widely accepted standard for synthesizing new 3D object views from a small number of base images. However, NeRFs have limited generalization properties, which means that we need to use significant computational resources to train individual architectures for each item we want to represent. To address this issue, we propose a few-shot learning approach based on the hypernetwork paradigm that does not require gradient optimization during inference. The hypernetwork gathers information from the training data and generates an update for universal weights. As a result, we have developed an efficient method for generating a high-quality 3D object representation from a small number of images in a single step. This has been confirmed by direct comparison with the state-of-the-art solutions and a comprehensive ablation study.

Bounding Evidence and Estimating Log-Likelihood in VAE

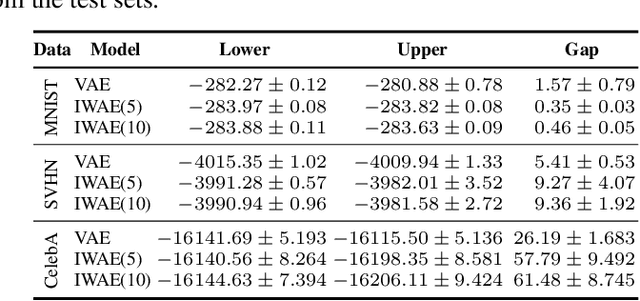
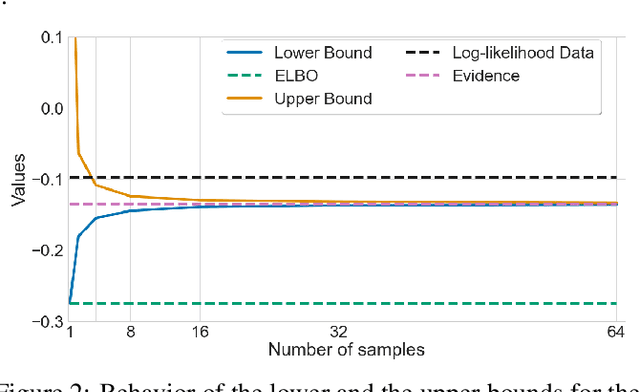
Many crucial problems in deep learning and statistics are caused by a variational gap, i.e., a difference between evidence and evidence lower bound (ELBO). As a consequence, in the classical VAE model, we obtain only the lower bound on the log-likelihood since ELBO is used as a cost function, and therefore we cannot compare log-likelihood between models. In this paper, we present a general and effective upper bound of the variational gap, which allows us to efficiently estimate the true evidence. We provide an extensive theoretical study of the proposed approach. Moreover, we show that by applying our estimation, we can easily obtain lower and upper bounds for the log-likelihood of VAE models.

Target Layer Regularization for Continual Learning Using Cramer-Wold Generator

We propose an effective regularization strategy (CW-TaLaR) for solving continual learning problems. It uses a penalizing term expressed by the Cramer-Wold distance between two probability distributions defined on a target layer of an underlying neural network that is shared by all tasks, and the simple architecture of the Cramer-Wold generator for modeling output data representation. Our strategy preserves target layer distribution while learning a new task but does not require remembering previous tasks' datasets. We perform experiments involving several common supervised frameworks, which prove the competitiveness of the CW-TaLaR method in comparison to a few existing state-of-the-art continual learning models.

HyperCube: Implicit Field Representations of Voxelized 3D Models

Recently introduced implicit field representations offer an effective way of generating 3D object shapes. They leverage implicit decoder trained to take a 3D point coordinate concatenated with a shape encoding and to output a value which indicates whether the point is outside the shape or not. Although this approach enables efficient rendering of visually plausible objects, it has two significant limitations. First, it is based on a single neural network dedicated for all objects from a training set which results in a cumbersome training procedure and its application in real life. More importantly, the implicit decoder takes only points sampled within voxels (and not the entire voxels) which yields problems at the classification boundaries and results in empty spaces within the rendered mesh. To solve the above limitations, we introduce a new HyperCube architecture based on interval arithmetic network, that enables direct processing of 3D voxels, trained using a hypernetwork paradigm to enforce model convergence. Instead of processing individual 3D samples from within a voxel, our approach allows to input the entire voxel (3D cube) represented with its convex hull coordinates, while the target network constructed by a hypernet assigns it to an inside or outside category. As a result our HyperCube model outperforms the competing approaches both in terms of training and inference efficiency, as well as the final mesh quality.