Bounding Evidence and Estimating Log-Likelihood in VAE
Paper and Code
Jun 19, 2022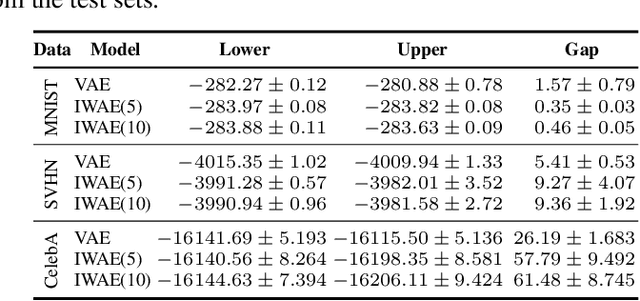
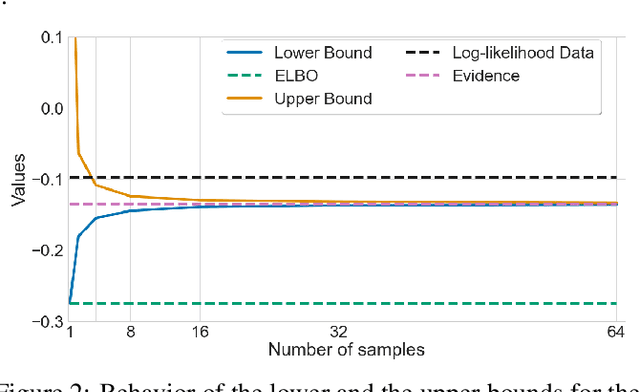


Many crucial problems in deep learning and statistics are caused by a variational gap, i.e., a difference between evidence and evidence lower bound (ELBO). As a consequence, in the classical VAE model, we obtain only the lower bound on the log-likelihood since ELBO is used as a cost function, and therefore we cannot compare log-likelihood between models. In this paper, we present a general and effective upper bound of the variational gap, which allows us to efficiently estimate the true evidence. We provide an extensive theoretical study of the proposed approach. Moreover, we show that by applying our estimation, we can easily obtain lower and upper bounds for the log-likelihood of VAE models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge