HuSc3D: Human Sculpture dataset for 3D object reconstruction

3D scene reconstruction from 2D images is one of the most important tasks in computer graphics. Unfortunately, existing datasets and benchmarks concentrate on idealized synthetic or meticulously captured realistic data. Such benchmarks fail to convey the inherent complexities encountered in newly acquired real-world scenes. In such scenes especially those acquired outside, the background is often dynamic, and by popular usage of cell phone cameras, there might be discrepancies in, e.g., white balance. To address this gap, we present HuSc3D, a novel dataset specifically designed for rigorous benchmarking of 3D reconstruction models under realistic acquisition challenges. Our dataset uniquely features six highly detailed, fully white sculptures characterized by intricate perforations and minimal textural and color variation. Furthermore, the number of images per scene varies significantly, introducing the additional challenge of limited training data for some instances alongside scenes with a standard number of views. By evaluating popular 3D reconstruction methods on this diverse dataset, we demonstrate the distinctiveness of HuSc3D in effectively differentiating model performance, particularly highlighting the sensitivity of methods to fine geometric details, color ambiguity, and varying data availability--limitations often masked by more conventional datasets.

CLIPGaussian: Universal and Multimodal Style Transfer Based on Gaussian Splatting

Gaussian Splatting (GS) has recently emerged as an efficient representation for rendering 3D scenes from 2D images and has been extended to images, videos, and dynamic 4D content. However, applying style transfer to GS-based representations, especially beyond simple color changes, remains challenging. In this work, we introduce CLIPGaussians, the first unified style transfer framework that supports text- and image-guided stylization across multiple modalities: 2D images, videos, 3D objects, and 4D scenes. Our method operates directly on Gaussian primitives and integrates into existing GS pipelines as a plug-in module, without requiring large generative models or retraining from scratch. CLIPGaussians approach enables joint optimization of color and geometry in 3D and 4D settings, and achieves temporal coherence in videos, while preserving a model size. We demonstrate superior style fidelity and consistency across all tasks, validating CLIPGaussians as a universal and efficient solution for multimodal style transfer.

EPIC: Explanation of Pretrained Image Classification Networks via Prototype

Explainable AI (XAI) methods generally fall into two categories. Post-hoc approaches generate explanations for pre-trained models and are compatible with various neural network architectures. These methods often use feature importance visualizations, such as saliency maps, to indicate which input regions influenced the model's prediction. Unfortunately, they typically offer a coarse understanding of the model's decision-making process. In contrast, ante-hoc (inherently explainable) methods rely on specially designed model architectures trained from scratch. A notable subclass of these methods provides explanations through prototypes, representative patches extracted from the training data. However, prototype-based approaches have limitations: they require dedicated architectures, involve specialized training procedures, and perform well only on specific datasets. In this work, we propose EPIC (Explanation of Pretrained Image Classification), a novel approach that bridges the gap between these two paradigms. Like post-hoc methods, EPIC operates on pre-trained models without architectural modifications. Simultaneously, it delivers intuitive, prototype-based explanations inspired by ante-hoc techniques. To the best of our knowledge, EPIC is the first post-hoc method capable of fully replicating the core explanatory power of inherently interpretable models. We evaluate EPIC on benchmark datasets commonly used in prototype-based explanations, such as CUB-200-2011 and Stanford Cars, alongside large-scale datasets like ImageNet, typically employed by post-hoc methods. EPIC uses prototypes to explain model decisions, providing a flexible and easy-to-understand tool for creating clear, high-quality explanations.

REdiSplats: Ray Tracing for Editable Gaussian Splatting

Gaussian Splatting (GS) has become one of the most important neural rendering algorithms. GS represents 3D scenes using Gaussian components with trainable color and opacity. This representation achieves high-quality renderings with fast inference. Regrettably, it is challenging to integrate such a solution with varying light conditions, including shadows and light reflections, manual adjustments, and a physical engine. Recently, a few approaches have appeared that incorporate ray-tracing or mesh primitives into GS to address some of these caveats. However, no such solution can simultaneously solve all the existing limitations of the classical GS. Consequently, we introduce REdiSplats, which employs ray tracing and a mesh-based representation of flat 3D Gaussians. In practice, we model the scene using flat Gaussian distributions parameterized by the mesh. We can leverage fast ray tracing and control Gaussian modification by adjusting the mesh vertices. Moreover, REdiSplats allows modeling of light conditions, manual adjustments, and physical simulation. Furthermore, we can render our models using 3D tools such as Blender or Nvdiffrast, which opens the possibility of integrating them with all existing 3D graphics techniques dedicated to mesh representations.

MiraGe: Editable 2D Images using Gaussian Splatting

Implicit Neural Representations (INRs) approximate discrete data through continuous functions and are commonly used for encoding 2D images. Traditional image-based INRs employ neural networks to map pixel coordinates to RGB values, capturing shapes, colors, and textures within the network's weights. Recently, GaussianImage has been proposed as an alternative, using Gaussian functions instead of neural networks to achieve comparable quality and compression. Such a solution obtains a quality and compression ratio similar to classical INR models but does not allow image modification. In contrast, our work introduces a novel method, MiraGe, which uses mirror reflections to perceive 2D images in 3D space and employs flat-controlled Gaussians for precise 2D image editing. Our approach improves the rendering quality and allows realistic image modifications, including human-inspired perception of photos in the 3D world. Thanks to modeling images in 3D space, we obtain the illusion of 3D-based modification in 2D images. We also show that our Gaussian representation can be easily combined with a physics engine to produce physics-based modification of 2D images. Consequently, MiraGe allows for better quality than the standard approach and natural modification of 2D images.

GASP: Gaussian Splatting for Physic-Based Simulations

Physics simulation is paramount for modeling and utilization of 3D scenes in various real-world applications. However, its integration with state-of-the-art 3D scene rendering techniques such as Gaussian Splatting (GS) remains challenging. Existing models use additional meshing mechanisms, including triangle or tetrahedron meshing, marching cubes, or cage meshes. As an alternative, we can modify the physics grounded Newtonian dynamics to align with 3D Gaussian components. Current models take the first-order approximation of a deformation map, which locally approximates the dynamics by linear transformations. In contrast, our Gaussian Splatting for Physics-Based Simulations (GASP) model uses such a map (without any modifications) and flat Gaussian distributions, which are parameterized by three points (mesh faces). Subsequently, each 3D point (mesh face node) is treated as a discrete entity within a 3D space. Consequently, the problem of modeling Gaussian components is reduced to working with 3D points. Additionally, the information on mesh faces can be used to incorporate further properties into the physics model, facilitating the use of triangles. Resulting solution can be integrated into any physics engine that can be treated as a black box. As demonstrated in our studies, the proposed model exhibits superior performance on a diverse range of benchmark datasets designed for 3D object rendering.

D-MiSo: Editing Dynamic 3D Scenes using Multi-Gaussians Soup

Over the past years, we have observed an abundance of approaches for modeling dynamic 3D scenes using Gaussian Splatting (GS). Such solutions use GS to represent the scene's structure and the neural network to model dynamics. Such approaches allow fast rendering and extracting each element of such a dynamic scene. However, modifying such objects over time is challenging. SC-GS (Sparse Controlled Gaussian Splatting) enhanced with Deformed Control Points partially solves this issue. However, this approach necessitates selecting elements that need to be kept fixed, as well as centroids that should be adjusted throughout editing. Moreover, this task poses additional difficulties regarding the re-productivity of such editing. To address this, we propose Dynamic Multi-Gaussian Soup (D-MiSo), which allows us to model the mesh-inspired representation of dynamic GS. Additionally, we propose a strategy of linking parameterized Gaussian splats, forming a Triangle Soup with the estimated mesh. Consequently, we can separately construct new trajectories for the 3D objects composing the scene. Thus, we can make the scene's dynamic editable over time or while maintaining partial dynamics.

GaMeS: Mesh-Based Adapting and Modification of Gaussian Splatting

Recently, a range of neural network-based methods for image rendering have been introduced. One such widely-researched neural radiance field (NeRF) relies on a neural network to represent 3D scenes, allowing for realistic view synthesis from a small number of 2D images. However, most NeRF models are constrained by long training and inference times. In comparison, Gaussian Splatting (GS) is a novel, state-of-the-art technique for rendering points in a 3D scene by approximating their contribution to image pixels through Gaussian distributions, warranting fast training and swift, real-time rendering. A drawback of GS is the absence of a well-defined approach for its conditioning due to the necessity to condition several hundred thousand Gaussian components. To solve this, we introduce the Gaussian Mesh Splatting (GaMeS) model, which allows modification of Gaussian components in a similar way as meshes. We parameterize each Gaussian component by the vertices of the mesh face. Furthermore, our model needs mesh initialization on input or estimated mesh during training. We also define Gaussian splats solely based on their location on the mesh, allowing for automatic adjustments in position, scale, and rotation during animation. As a result, we obtain a real-time rendering of editable GS.

Hypernetwork approach to Bayesian MAML

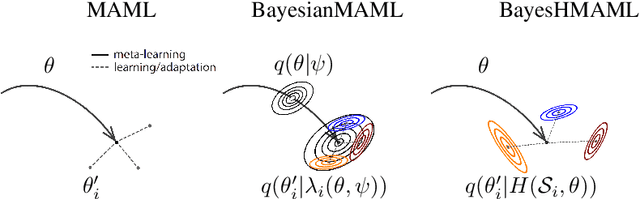
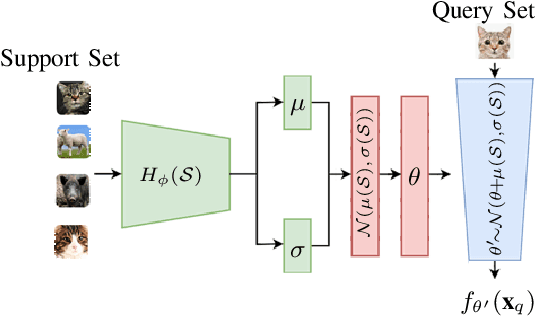
The main goal of Few-Shot learning algorithms is to enable learning from small amounts of data. One of the most popular and elegant Few-Shot learning approaches is Model-Agnostic Meta-Learning (MAML). The main idea behind this method is to learn shared universal weights of a meta-model, which then are adapted for specific tasks. However, due to limited data size, the method suffers from over-fitting and poorly quantifies uncertainty. Bayesian approaches could, in principle, alleviate these shortcomings by learning weight distributions in place of point-wise weights. Unfortunately, previous Bayesian modifications of MAML are limited in a way similar to the classic MAML, e.g., task-specific adaptations must share the same structure and can not diverge much from the universal meta-model. Additionally, task-specific distributions are considered as posteriors to the universal distributions working as priors, and optimizing them jointly with gradients is hard and poses a risk of getting stuck in local optima. In this paper, we propose BayesianHyperShot, a novel generalization of Bayesian MAML, which employs Bayesian principles along with Hypernetworks for MAML. We achieve better convergence than the previous methods by classically learning universal weights. Furthermore, Bayesian treatment of the specific tasks enables uncertainty quantification, and high flexibility of task adaptations is achieved using Hypernetworks instead of gradient-based updates. Consequently, the proposed approach not only improves over the previous methods, both classic and Bayesian MAML in several standard Few-Shot learning benchmarks but also benefits from the properties of the Bayesian framework.