TACTIC for Navigating the Unknown: Tabular Anomaly deteCTion via In-Context inference

Anomaly detection for tabular data has been a long-standing unsupervised learning problem that remains a major challenge for current deep learning models. Recently, in-context learning has emerged as a new paradigm that has shifted efforts from task-specific optimization to large-scale pretraining aimed at creating foundation models that generalize across diverse datasets. Although in-context models, such as TabPFN, perform well in supervised problems, their learned classification-based priors may not readily extend to anomaly detection. In this paper, we study in-context models for anomaly detection and show that the unsupervised extensions to TabPFN exhibit unstable behavior, particularly in noisy or contaminated contexts, in addition to the high computational cost. We address these challenges and introduce TACTIC, an in-context anomaly detection approach based on pretraining with anomaly-centric synthetic priors, which provides fast and data-dependent reasoning about anomalies while avoiding dataset-specific tuning. In contrast to typical score-based approaches, which produce uncalibrated anomaly scores that require post-processing (e.g. threshold selection or ranking heuristics), the proposed model is trained as a discriminative predictor, enabling unambiguous anomaly decisions in a single forward pass. Through experiments on real-world datasets, we examine the performance of TACTIC in clean and noisy contexts with varying anomaly rates and different anomaly types, as well as the impact of prior choices on detection quality. Our experiments clearly show that specialized anomaly-centric in-context models such as TACTIC are highly competitive compared to other task-specific methods.

Hi-fi functional priors by learning activations

Function-space priors in Bayesian Neural Networks (BNNs) provide a more intuitive approach to embedding beliefs directly into the model's output, thereby enhancing regularization, uncertainty quantification, and risk-aware decision-making. However, imposing function-space priors on BNNs is challenging. We address this task through optimization techniques that explore how trainable activations can accommodate higher-complexity priors and match intricate target function distributions. We investigate flexible activation models, including Pade functions and piecewise linear functions, and discuss the learning challenges related to identifiability, loss construction, and symmetries. Our empirical findings indicate that even BNNs with a single wide hidden layer when equipped with flexible trainable activation, can effectively achieve desired function-space priors.

ZEUS: Zero-shot Embeddings for Unsupervised Separation of Tabular Data

Clustering tabular data remains a significant open challenge in data analysis and machine learning. Unlike for image data, similarity between tabular records often varies across datasets, making the definition of clusters highly dataset-dependent. Furthermore, the absence of supervised signals complicates hyperparameter tuning in deep learning clustering methods, frequently resulting in unstable performance. To address these issues and reduce the need for per-dataset tuning, we adopt an emerging approach in deep learning: zero-shot learning. We propose ZEUS, a self-contained model capable of clustering new datasets without any additional training or fine-tuning. It operates by decomposing complex datasets into meaningful components that can then be clustered effectively. Thanks to pre-training on synthetic datasets generated from a latent-variable prior, it generalizes across various datasets without requiring user intervention. To the best of our knowledge, ZEUS is the first zero-shot method capable of generating embeddings for tabular data in a fully unsupervised manner. Experimental results demonstrate that it performs on par with or better than traditional clustering algorithms and recent deep learning-based methods, while being significantly faster and more user-friendly.

Minimal Ranks, Maximum Confidence: Parameter-efficient Uncertainty Quantification for LoRA

Low-Rank Adaptation (LoRA) enables parameter-efficient fine-tuning of large language models by decomposing weight updates into low-rank matrices, significantly reducing storage and computational overhead. While effective, standard LoRA lacks mechanisms for uncertainty quantification, leading to overconfident and poorly calibrated models. Bayesian variants of LoRA address this limitation, but at the cost of a significantly increased number of trainable parameters, partially offsetting the original efficiency gains. Additionally, these models are harder to train and may suffer from unstable convergence. In this work, we propose a novel parameter-efficient Bayesian LoRA, demonstrating that effective uncertainty quantification can be achieved in very low-dimensional parameter spaces. The proposed method achieves strong performance with improved calibration and generalization while maintaining computational efficiency. Our empirical findings show that, with the appropriate projection of the weight space: (1) uncertainty can be effectively modeled in a low-dimensional space, and (2) weight covariances exhibit low ranks.

High-Fidelity Transfer of Functional Priors for Wide Bayesian Neural Networks by Learning Activations

Function-space priors in Bayesian Neural Networks provide a more intuitive approach to embedding beliefs directly into the model's output, thereby enhancing regularization, uncertainty quantification, and risk-aware decision-making. However, imposing function-space priors on BNNs is challenging. We address this task through optimization techniques that explore how trainable activations can accommodate complex priors and match intricate target function distributions. We discuss critical learning challenges, including identifiability, loss construction, and symmetries that arise in this context. Furthermore, we enable evidence maximization to facilitate model selection by conditioning the functional priors on additional hyperparameters. Our empirical findings demonstrate that even BNNs with a single wide hidden layer, when equipped with these adaptive trainable activations and conditioning strategies, can effectively achieve high-fidelity function-space priors, providing a robust and flexible framework for enhancing Bayesian neural network performance.

Hypernetwork approach to Bayesian MAML

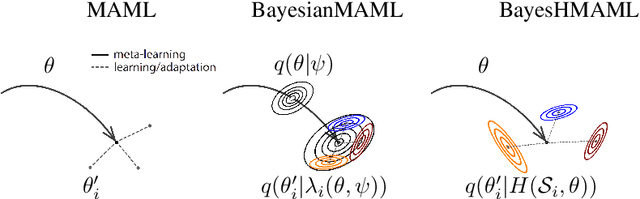
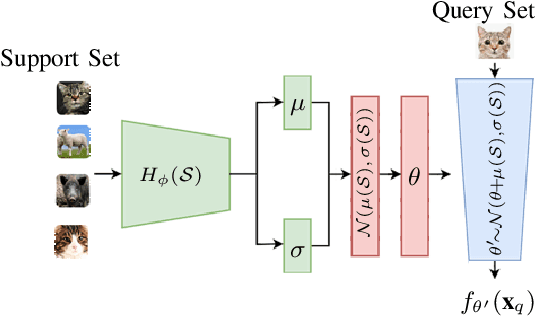
The main goal of Few-Shot learning algorithms is to enable learning from small amounts of data. One of the most popular and elegant Few-Shot learning approaches is Model-Agnostic Meta-Learning (MAML). The main idea behind this method is to learn shared universal weights of a meta-model, which then are adapted for specific tasks. However, due to limited data size, the method suffers from over-fitting and poorly quantifies uncertainty. Bayesian approaches could, in principle, alleviate these shortcomings by learning weight distributions in place of point-wise weights. Unfortunately, previous Bayesian modifications of MAML are limited in a way similar to the classic MAML, e.g., task-specific adaptations must share the same structure and can not diverge much from the universal meta-model. Additionally, task-specific distributions are considered as posteriors to the universal distributions working as priors, and optimizing them jointly with gradients is hard and poses a risk of getting stuck in local optima. In this paper, we propose BayesianHyperShot, a novel generalization of Bayesian MAML, which employs Bayesian principles along with Hypernetworks for MAML. We achieve better convergence than the previous methods by classically learning universal weights. Furthermore, Bayesian treatment of the specific tasks enables uncertainty quantification, and high flexibility of task adaptations is achieved using Hypernetworks instead of gradient-based updates. Consequently, the proposed approach not only improves over the previous methods, both classic and Bayesian MAML in several standard Few-Shot learning benchmarks but also benefits from the properties of the Bayesian framework.

Mixture of Discrete Normalizing Flows for Variational Inference

Advances in gradient-based inference have made distributional approximations for posterior distribution of latent-variable models easy, but only for continuous latent spaces. Models with discrete latent variables still require analytic marginalization, continuous relaxations, or specialized algorithms that are difficult to generalize already for minor variations of the model. Discrete normalizing flows could, in principle, be used as approximations while allowing efficient gradient-based learning, but as explained in this work they are not sufficiently expressive for representing realistic posterior distributions even for simple cases. We overcome this limitation by considering mixtures of discrete normalizing flows instead, and present a novel algorithm for modeling the posterior distribution of models with discrete latent variables, based on boosting variational inference.

Prior specification via prior predictive matching: Poisson matrix factorization and beyond

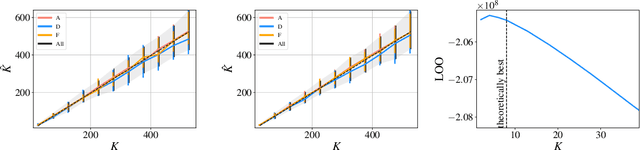
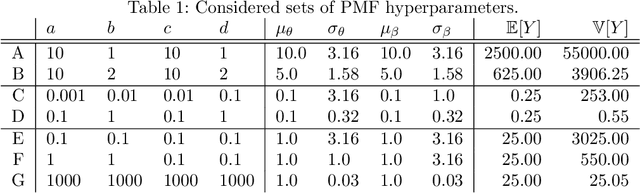
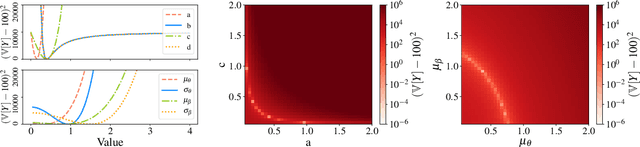
Hyperparameter optimization for machine learning models is typically carried out by some sort of cross-validation procedure or global optimization, both of which require running the learning algorithm numerous times. We show that for Bayesian hierarchical models there is an appealing alternative that allows selecting good hyperparameters without learning the model parameters during the process at all, facilitated by the prior predictive distribution that marginalizes out the model parameters. We propose an approach that matches suitable statistics of the prior predictive distribution with ones provided by an expert and apply the general concept for matrix factorization models. For some Poisson matrix factorization models we can analytically obtain exact hyperparameters, including the number of factors, and for more complex models we propose a model-independent optimization procedure.

Correcting Predictions for Approximate Bayesian Inference

Bayesian models quantify uncertainty and facilitate optimal decision-making in downstream applications. For most models, however, practitioners are forced to use approximate inference techniques that lead to sub-optimal decisions due to incorrect posterior predictive distributions. We present a novel approach that corrects for inaccuracies in posterior inference by altering the decision-making process. We train a separate model to make optimal decisions under the approximate posterior, combining interpretable Bayesian modeling with optimization of direct predictive accuracy in a principled fashion. The solution is generally applicable as a plug-in module for predictive decision-making for arbitrary probabilistic programs, irrespective of the posterior inference strategy. We demonstrate the approach empirically in several problems, confirming its potential.

Variational Bayesian Decision-making for Continuous Utilities

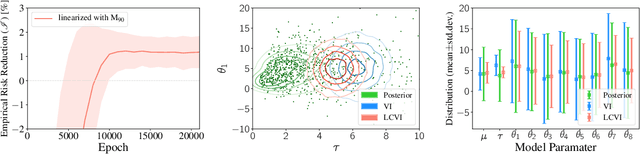
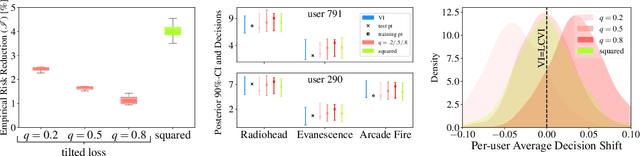
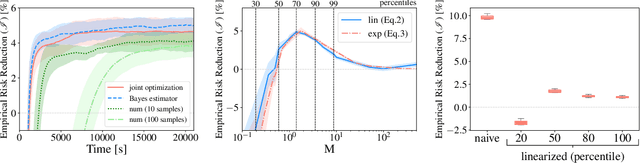
Bayesian decision theory outlines a rigorous framework for making optimal decisions based on maximizing expected utility over a model posterior. However, practitioners often do not have access to the full posterior and resort to approximate inference strategies. In such cases, taking the eventual decision-making task into account while performing the inference allows for calibrating the posterior approximation to maximize the utility. We present an automatic pipeline that co-opts continuous utilities into variational inference algorithms to account for decision-making. We provide practical strategies for approximating and maximizing gain, and empirically demonstrate consistent improvement when calibrating approximations for specific utilities.