On Divergence Measures for Training GFlowNets

Generative Flow Networks (GFlowNets) are amortized inference models designed to sample from unnormalized distributions over composable objects, with applications in generative modeling for tasks in fields such as causal discovery, NLP, and drug discovery. Traditionally, the training procedure for GFlowNets seeks to minimize the expected log-squared difference between a proposal (forward policy) and a target (backward policy) distribution, which enforces certain flow-matching conditions. While this training procedure is closely related to variational inference (VI), directly attempting standard Kullback-Leibler (KL) divergence minimization can lead to proven biased and potentially high-variance estimators. Therefore, we first review four divergence measures, namely, Renyi-$\alpha$'s, Tsallis-$\alpha$'s, reverse and forward KL's, and design statistically efficient estimators for their stochastic gradients in the context of training GFlowNets. Then, we verify that properly minimizing these divergences yields a provably correct and empirically effective training scheme, often leading to significantly faster convergence than previously proposed optimization. To achieve this, we design control variates based on the REINFORCE leave-one-out and score-matching estimators to reduce the variance of the learning objectives' gradients. Our work contributes by narrowing the gap between GFlowNets training and generalized variational approximations, paving the way for algorithmic ideas informed by the divergence minimization viewpoint.

Prior specification via prior predictive matching: Poisson matrix factorization and beyond

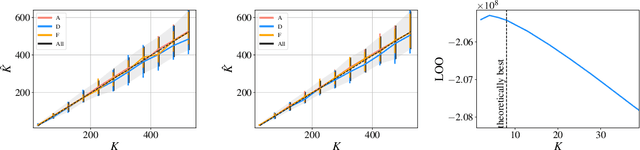
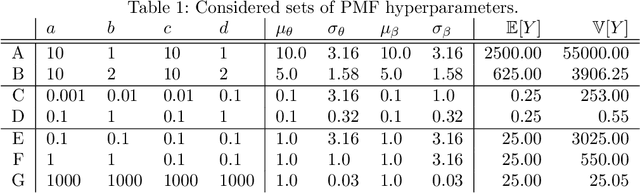
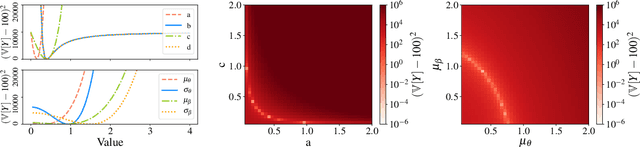
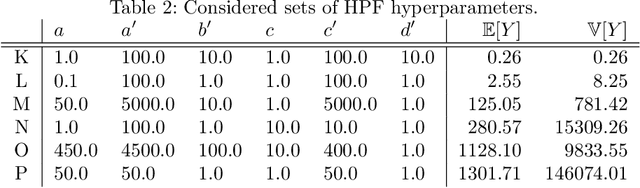
Hyperparameter optimization for machine learning models is typically carried out by some sort of cross-validation procedure or global optimization, both of which require running the learning algorithm numerous times. We show that for Bayesian hierarchical models there is an appealing alternative that allows selecting good hyperparameters without learning the model parameters during the process at all, facilitated by the prior predictive distribution that marginalizes out the model parameters. We propose an approach that matches suitable statistics of the prior predictive distribution with ones provided by an expert and apply the general concept for matrix factorization models. For some Poisson matrix factorization models we can analytically obtain exact hyperparameters, including the number of factors, and for more complex models we propose a model-independent optimization procedure.

Augmented Memory Networks for Streaming-Based Active One-Shot Learning

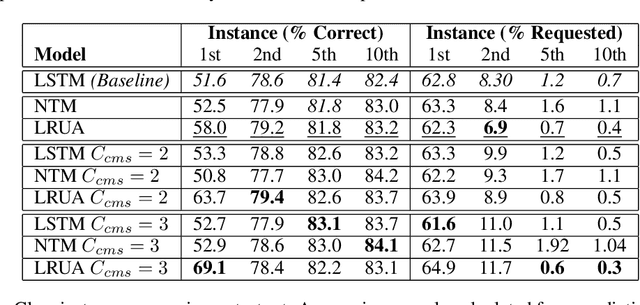
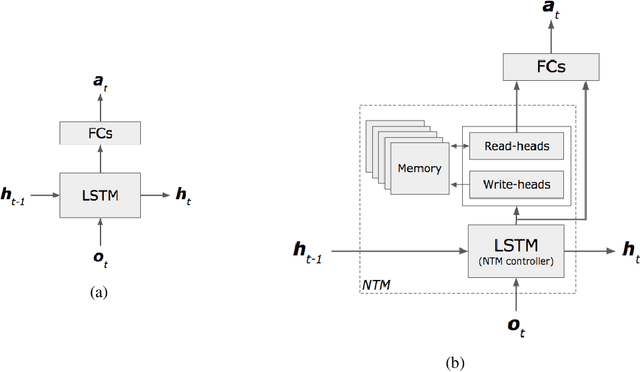
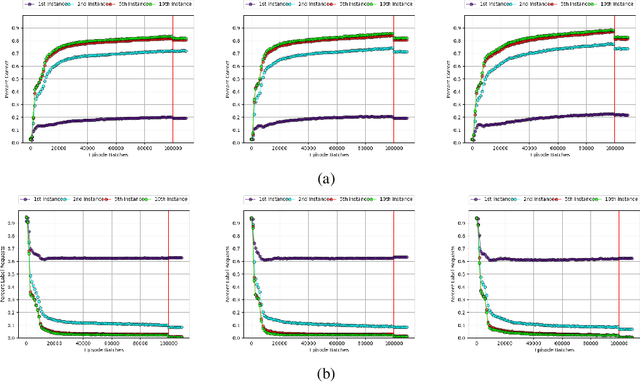
One of the major challenges in training deep architectures for predictive tasks is the scarcity and cost of labeled training data. Active Learning (AL) is one way of addressing this challenge. In stream-based AL, observations are continuously made available to the learner that have to decide whether to request a label or to make a prediction. The goal is to reduce the request rate while at the same time maximize prediction performance. In previous research, reinforcement learning has been used for learning the AL request/prediction strategy. In our work, we propose to equip a reinforcement learning process with memory augmented neural networks, to enhance the one-shot capabilities. Moreover, we introduce Class Margin Sampling (CMS) as an extension of the standard margin sampling to the reinforcement learning setting. This strategy aims to reduce training time and improve sample efficiency in the training process. We evaluate the proposed method on a classification task using empirical accuracy of label predictions and percentage of label requests. The results indicates that the proposed method, by making use of the memory augmented networks and CMS in the training process, outperforms existing baselines.