Streaming Bayes GFlowNets

Bayes' rule naturally allows for inference refinement in a streaming fashion, without the need to recompute posteriors from scratch whenever new data arrives. In principle, Bayesian streaming is straightforward: we update our prior with the available data and use the resulting posterior as a prior when processing the next data chunk. In practice, however, this recipe entails i) approximating an intractable posterior at each time step; and ii) encapsulating results appropriately to allow for posterior propagation. For continuous state spaces, variational inference (VI) is particularly convenient due to its scalability and the tractability of variational posteriors. For discrete state spaces, however, state-of-the-art VI results in analytically intractable approximations that are ill-suited for streaming settings. To enable streaming Bayesian inference over discrete parameter spaces, we propose streaming Bayes GFlowNets (abbreviated as SB-GFlowNets) by leveraging the recently proposed GFlowNets -- a powerful class of amortized samplers for discrete compositional objects. Notably, SB-GFlowNet approximates the initial posterior using a standard GFlowNet and subsequently updates it using a tailored procedure that requires only the newly observed data. Our case studies in linear preference learning and phylogenetic inference showcase the effectiveness of SB-GFlowNets in sampling from an unnormalized posterior in a streaming setting. As expected, we also observe that SB-GFlowNets is significantly faster than repeatedly training a GFlowNet from scratch to sample from the full posterior.

On Divergence Measures for Training GFlowNets

Generative Flow Networks (GFlowNets) are amortized inference models designed to sample from unnormalized distributions over composable objects, with applications in generative modeling for tasks in fields such as causal discovery, NLP, and drug discovery. Traditionally, the training procedure for GFlowNets seeks to minimize the expected log-squared difference between a proposal (forward policy) and a target (backward policy) distribution, which enforces certain flow-matching conditions. While this training procedure is closely related to variational inference (VI), directly attempting standard Kullback-Leibler (KL) divergence minimization can lead to proven biased and potentially high-variance estimators. Therefore, we first review four divergence measures, namely, Renyi-$\alpha$'s, Tsallis-$\alpha$'s, reverse and forward KL's, and design statistically efficient estimators for their stochastic gradients in the context of training GFlowNets. Then, we verify that properly minimizing these divergences yields a provably correct and empirically effective training scheme, often leading to significantly faster convergence than previously proposed optimization. To achieve this, we design control variates based on the REINFORCE leave-one-out and score-matching estimators to reduce the variance of the learning objectives' gradients. Our work contributes by narrowing the gap between GFlowNets training and generalized variational approximations, paving the way for algorithmic ideas informed by the divergence minimization viewpoint.

Embarrassingly Parallel GFlowNets

GFlowNets are a promising alternative to MCMC sampling for discrete compositional random variables. Training GFlowNets requires repeated evaluations of the unnormalized target distribution or reward function. However, for large-scale posterior sampling, this may be prohibitive since it incurs traversing the data several times. Moreover, if the data are distributed across clients, employing standard GFlowNets leads to intensive client-server communication. To alleviate both these issues, we propose embarrassingly parallel GFlowNet (EP-GFlowNet). EP-GFlowNet is a provably correct divide-and-conquer method to sample from product distributions of the form $R(\cdot) \propto R_1(\cdot) ... R_N(\cdot)$ -- e.g., in parallel or federated Bayes, where each $R_n$ is a local posterior defined on a data partition. First, in parallel, we train a local GFlowNet targeting each $R_n$ and send the resulting models to the server. Then, the server learns a global GFlowNet by enforcing our newly proposed \emph{aggregating balance} condition, requiring a single communication step. Importantly, EP-GFlowNets can also be applied to multi-objective optimization and model reuse. Our experiments illustrate the EP-GFlowNets's effectiveness on many tasks, including parallel Bayesian phylogenetics, multi-objective multiset, sequence generation, and federated Bayesian structure learning.

Human-in-the-Loop Causal Discovery under Latent Confounding using Ancestral GFlowNets

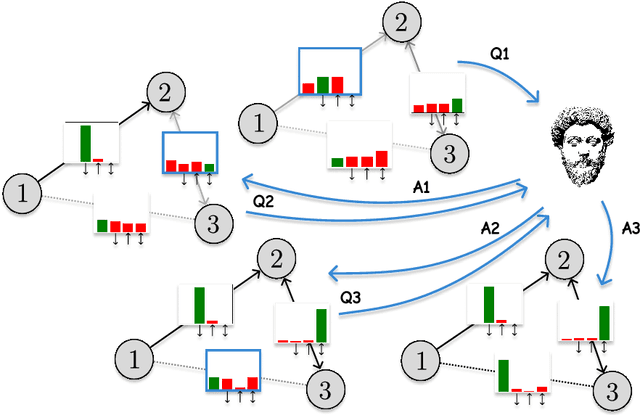
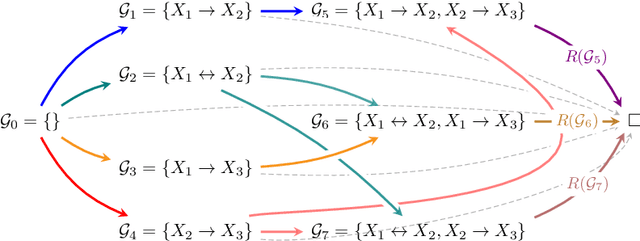
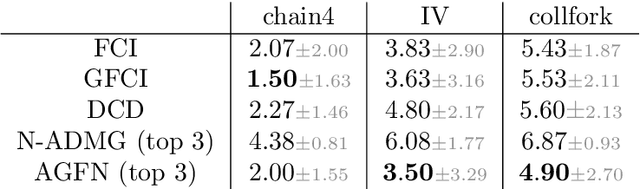
Structure learning is the crux of causal inference. Notably, causal discovery (CD) algorithms are brittle when data is scarce, possibly inferring imprecise causal relations that contradict expert knowledge -- especially when considering latent confounders. To aggravate the issue, most CD methods do not provide uncertainty estimates, making it hard for users to interpret results and improve the inference process. Surprisingly, while CD is a human-centered affair, no works have focused on building methods that both 1) output uncertainty estimates that can be verified by experts and 2) interact with those experts to iteratively refine CD. To solve these issues, we start by proposing to sample (causal) ancestral graphs proportionally to a belief distribution based on a score function, such as the Bayesian information criterion (BIC), using generative flow networks. Then, we leverage the diversity in candidate graphs and introduce an optimal experimental design to iteratively probe the expert about the relations among variables, effectively reducing the uncertainty of our belief over ancestral graphs. Finally, we update our samples to incorporate human feedback via importance sampling. Importantly, our method does not require causal sufficiency (i.e., unobserved confounders may exist). Experiments with synthetic observational data show that our method can accurately sample from distributions over ancestral graphs and that we can greatly improve inference quality with human aid.