Boosted GFlowNets: Improving Exploration via Sequential Learning

Generative Flow Networks (GFlowNets) are powerful samplers for compositional objects that, by design, sample proportionally to a given non-negative reward. Nonetheless, in practice, they often struggle to explore the reward landscape evenly: trajectories toward easy-to-reach regions dominate training, while hard-to-reach modes receive vanishing or uninformative gradients, leading to poor coverage of high-reward areas. We address this imbalance with Boosted GFlowNets, a method that sequentially trains an ensemble of GFlowNets, each optimizing a residual reward that compensates for the mass already captured by previous models. This residual principle reactivates learning signals in underexplored regions and, under mild assumptions, ensures a monotone non-degradation property: adding boosters cannot worsen the learned distribution and typically improves it. Empirically, Boosted GFlowNets achieve substantially better exploration and sample diversity on multimodal synthetic benchmarks and peptide design tasks, while preserving the stability and simplicity of standard trajectory-balance training.

When Can Proxies Improve the Sample Complexity of Preference Learning?

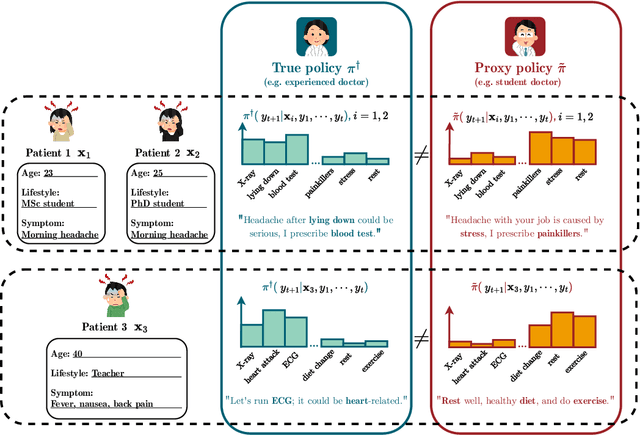
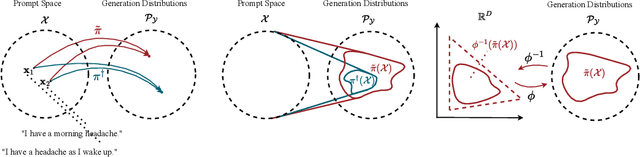
We address the problem of reward hacking, where maximising a proxy reward does not necessarily increase the true reward. This is a key concern for Large Language Models (LLMs), as they are often fine-tuned on human preferences that may not accurately reflect a true objective. Existing work uses various tricks such as regularisation, tweaks to the reward model, and reward hacking detectors, to limit the influence that such proxy preferences have on a model. Luckily, in many contexts such as medicine, education, and law, a sparse amount of expert data is often available. In these cases, it is often unclear whether the addition of proxy data can improve policy learning. We outline a set of sufficient conditions on proxy feedback that, if satisfied, indicate that proxy data can provably improve the sample complexity of learning the ground truth policy. These conditions can inform the data collection process for specific tasks. The result implies a parameterisation for LLMs that achieves this improved sample complexity. We detail how one can adapt existing architectures to yield this improved sample complexity.

Streaming Bayes GFlowNets

Bayes' rule naturally allows for inference refinement in a streaming fashion, without the need to recompute posteriors from scratch whenever new data arrives. In principle, Bayesian streaming is straightforward: we update our prior with the available data and use the resulting posterior as a prior when processing the next data chunk. In practice, however, this recipe entails i) approximating an intractable posterior at each time step; and ii) encapsulating results appropriately to allow for posterior propagation. For continuous state spaces, variational inference (VI) is particularly convenient due to its scalability and the tractability of variational posteriors. For discrete state spaces, however, state-of-the-art VI results in analytically intractable approximations that are ill-suited for streaming settings. To enable streaming Bayesian inference over discrete parameter spaces, we propose streaming Bayes GFlowNets (abbreviated as SB-GFlowNets) by leveraging the recently proposed GFlowNets -- a powerful class of amortized samplers for discrete compositional objects. Notably, SB-GFlowNet approximates the initial posterior using a standard GFlowNet and subsequently updates it using a tailored procedure that requires only the newly observed data. Our case studies in linear preference learning and phylogenetic inference showcase the effectiveness of SB-GFlowNets in sampling from an unnormalized posterior in a streaming setting. As expected, we also observe that SB-GFlowNets is significantly faster than repeatedly training a GFlowNet from scratch to sample from the full posterior.

Thin and Deep Gaussian Processes

Gaussian processes (GPs) can provide a principled approach to uncertainty quantification with easy-to-interpret kernel hyperparameters, such as the lengthscale, which controls the correlation distance of function values. However, selecting an appropriate kernel can be challenging. Deep GPs avoid manual kernel engineering by successively parameterizing kernels with GP layers, allowing them to learn low-dimensional embeddings of the inputs that explain the output data. Following the architecture of deep neural networks, the most common deep GPs warp the input space layer-by-layer but lose all the interpretability of shallow GPs. An alternative construction is to successively parameterize the lengthscale of a kernel, improving the interpretability but ultimately giving away the notion of learning lower-dimensional embeddings. Unfortunately, both methods are susceptible to particular pathologies which may hinder fitting and limit their interpretability. This work proposes a novel synthesis of both previous approaches: Thin and Deep GP (TDGP). Each TDGP layer defines locally linear transformations of the original input data maintaining the concept of latent embeddings while also retaining the interpretation of lengthscales of a kernel. Moreover, unlike the prior solutions, TDGP induces non-pathological manifolds that admit learning lower-dimensional representations. We show with theoretical and experimental results that i) TDGP is, unlike previous models, tailored to specifically discover lower-dimensional manifolds in the input data, ii) TDGP behaves well when increasing the number of layers, and iii) TDGP performs well in standard benchmark datasets.

Actually Sparse Variational Gaussian Processes

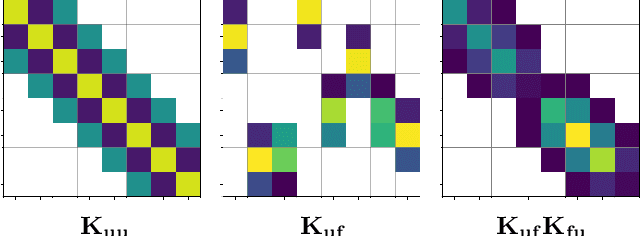
Gaussian processes (GPs) are typically criticised for their unfavourable scaling in both computational and memory requirements. For large datasets, sparse GPs reduce these demands by conditioning on a small set of inducing variables designed to summarise the data. In practice however, for large datasets requiring many inducing variables, such as low-lengthscale spatial data, even sparse GPs can become computationally expensive, limited by the number of inducing variables one can use. In this work, we propose a new class of inter-domain variational GP, constructed by projecting a GP onto a set of compactly supported B-spline basis functions. The key benefit of our approach is that the compact support of the B-spline basis functions admits the use of sparse linear algebra to significantly speed up matrix operations and drastically reduce the memory footprint. This allows us to very efficiently model fast-varying spatial phenomena with tens of thousands of inducing variables, where previous approaches failed.

Parallel MCMC Without Embarrassing Failures

Embarrassingly parallel Markov Chain Monte Carlo (MCMC) exploits parallel computing to scale Bayesian inference to large datasets by using a two-step approach. First, MCMC is run in parallel on (sub)posteriors defined on data partitions. Then, a server combines local results. While efficient, this framework is very sensitive to the quality of subposterior sampling. Common sampling problems such as missing modes or misrepresentation of low-density regions are amplified -- instead of being corrected -- in the combination phase, leading to catastrophic failures. In this work, we propose a novel combination strategy to mitigate this issue. Our strategy, Parallel Active Inference (PAI), leverages Gaussian Process (GP) surrogate modeling and active learning. After fitting GPs to subposteriors, PAI (i) shares information between GP surrogates to cover missing modes; and (ii) uses active sampling to individually refine subposterior approximations. We validate PAI in challenging benchmarks, including heavy-tailed and multi-modal posteriors and a real-world application to computational neuroscience. Empirical results show that PAI succeeds where previous methods catastrophically fail, with a small communication overhead.