Efficient Autoregressive Inference for Transformer Probabilistic Models

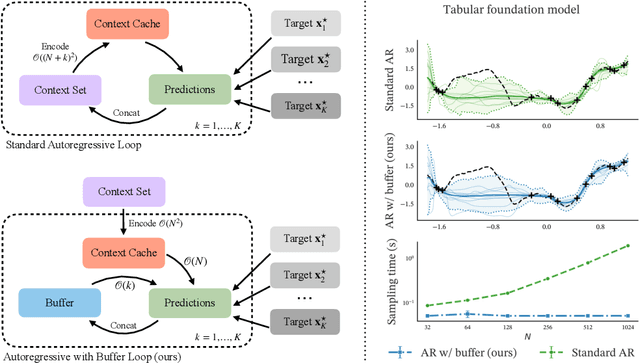
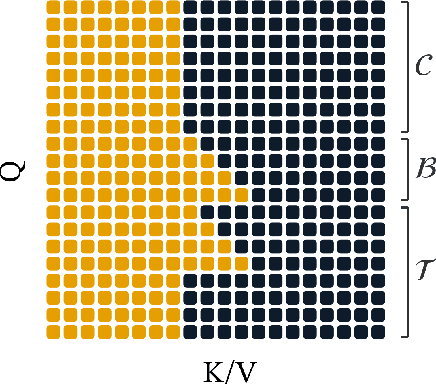
Transformer-based models for amortized probabilistic inference, such as neural processes, prior-fitted networks, and tabular foundation models, excel at single-pass marginal prediction. However, many real-world applications, from signal interpolation to multi-column tabular predictions, require coherent joint distributions that capture dependencies between predictions. While purely autoregressive architectures efficiently generate such distributions, they sacrifice the flexible set-conditioning that makes these models powerful for meta-learning. Conversely, the standard approach to obtain joint distributions from set-based models requires expensive re-encoding of the entire augmented conditioning set at each autoregressive step. We introduce a causal autoregressive buffer that preserves the advantages of both paradigms. Our approach decouples context encoding from updating the conditioning set. The model processes the context once and caches it. A dynamic buffer then captures target dependencies: as targets are incorporated, they enter the buffer and attend to both the cached context and previously buffered targets. This enables efficient batched autoregressive generation and one-pass joint log-likelihood evaluation. A unified training strategy allows seamless integration of set-based and autoregressive modes at minimal additional cost. Across synthetic functions, EEG signals, cognitive models, and tabular data, our method matches predictive accuracy of strong baselines while delivering up to 20 times faster joint sampling. Our approach combines the efficiency of autoregressive generative models with the representational power of set-based conditioning, making joint prediction practical for transformer-based probabilistic models.

Generative World Modelling for Humanoids: 1X World Model Challenge Technical Report

World models are a powerful paradigm in AI and robotics, enabling agents to reason about the future by predicting visual observations or compact latent states. The 1X World Model Challenge introduces an open-source benchmark of real-world humanoid interaction, with two complementary tracks: sampling, focused on forecasting future image frames, and compression, focused on predicting future discrete latent codes. For the sampling track, we adapt the video generation foundation model Wan-2.2 TI2V-5B to video-state-conditioned future frame prediction. We condition the video generation on robot states using AdaLN-Zero, and further post-train the model using LoRA. For the compression track, we train a Spatio-Temporal Transformer model from scratch. Our models achieve 23.0 dB PSNR in the sampling task and a Top-500 CE of 6.6386 in the compression task, securing 1st place in both challenges.

ALINE: Joint Amortization for Bayesian Inference and Active Data Acquisition

Many critical applications, from autonomous scientific discovery to personalized medicine, demand systems that can both strategically acquire the most informative data and instantaneously perform inference based upon it. While amortized methods for Bayesian inference and experimental design offer part of the solution, neither approach is optimal in the most general and challenging task, where new data needs to be collected for instant inference. To tackle this issue, we introduce the Amortized Active Learning and Inference Engine (ALINE), a unified framework for amortized Bayesian inference and active data acquisition. ALINE leverages a transformer architecture trained via reinforcement learning with a reward based on self-estimated information gain provided by its own integrated inference component. This allows it to strategically query informative data points while simultaneously refining its predictions. Moreover, ALINE can selectively direct its querying strategy towards specific subsets of model parameters or designated predictive tasks, optimizing for posterior estimation, data prediction, or a mixture thereof. Empirical results on regression-based active learning, classical Bayesian experimental design benchmarks, and a psychometric model with selectively targeted parameters demonstrate that ALINE delivers both instant and accurate inference along with efficient selection of informative points.

Normalizing Flow Regression for Bayesian Inference with Offline Likelihood Evaluations

Bayesian inference with computationally expensive likelihood evaluations remains a significant challenge in many scientific domains. We propose normalizing flow regression (NFR), a novel offline inference method for approximating posterior distributions. Unlike traditional surrogate approaches that require additional sampling or inference steps, NFR directly yields a tractable posterior approximation through regression on existing log-density evaluations. We introduce training techniques specifically for flow regression, such as tailored priors and likelihood functions, to achieve robust posterior and model evidence estimation. We demonstrate NFR's effectiveness on synthetic benchmarks and real-world applications from neuroscience and biology, showing superior or comparable performance to existing methods. NFR represents a promising approach for Bayesian inference when standard methods are computationally prohibitive or existing model evaluations can be recycled.

Stacking Variational Bayesian Monte Carlo

Variational Bayesian Monte Carlo (VBMC) is a sample-efficient method for approximate Bayesian inference with computationally expensive likelihoods. While VBMC's local surrogate approach provides stable approximations, its conservative exploration strategy and limited evaluation budget can cause it to miss regions of complex posteriors. In this work, we introduce Stacking Variational Bayesian Monte Carlo (S-VBMC), a method that constructs global posterior approximations by merging independent VBMC runs through a principled and inexpensive post-processing step. Our approach leverages VBMC's mixture posterior representation and per-component evidence estimates, requiring no additional likelihood evaluations while being naturally parallelizable. We demonstrate S-VBMC's effectiveness on two synthetic problems designed to challenge VBMC's exploration capabilities and two real-world applications from computational neuroscience, showing substantial improvements in posterior approximation quality across all cases.

Amortized Bayesian Experimental Design for Decision-Making

Many critical decisions, such as personalized medical diagnoses and product pricing, are made based on insights gained from designing, observing, and analyzing a series of experiments. This highlights the crucial role of experimental design, which goes beyond merely collecting information on system parameters as in traditional Bayesian experimental design (BED), but also plays a key part in facilitating downstream decision-making. Most recent BED methods use an amortized policy network to rapidly design experiments. However, the information gathered through these methods is suboptimal for down-the-line decision-making, as the experiments are not inherently designed with downstream objectives in mind. In this paper, we present an amortized decision-aware BED framework that prioritizes maximizing downstream decision utility. We introduce a novel architecture, the Transformer Neural Decision Process (TNDP), capable of instantly proposing the next experimental design, whilst inferring the downstream decision, thus effectively amortizing both tasks within a unified workflow. We demonstrate the performance of our method across several tasks, showing that it can deliver informative designs and facilitate accurate decision-making.

Amortized Probabilistic Conditioning for Optimization, Simulation and Inference

Amortized meta-learning methods based on pre-training have propelled fields like natural language processing and vision. Transformer-based neural processes and their variants are leading models for probabilistic meta-learning with a tractable objective. Often trained on synthetic data, these models implicitly capture essential latent information in the data-generation process. However, existing methods do not allow users to flexibly inject (condition on) and extract (predict) this probabilistic latent information at runtime, which is key to many tasks. We introduce the Amortized Conditioning Engine (ACE), a new transformer-based meta-learning model that explicitly represents latent variables of interest. ACE affords conditioning on both observed data and interpretable latent variables, the inclusion of priors at runtime, and outputs predictive distributions for discrete and continuous data and latents. We show ACE's modeling flexibility and performance in diverse tasks such as image completion and classification, Bayesian optimization, and simulation-based inference.

Preferential Normalizing Flows

Eliciting a high-dimensional probability distribution from an expert via noisy judgments is notoriously challenging, yet useful for many applications, such as prior elicitation and reward modeling. We introduce a method for eliciting the expert's belief density as a normalizing flow based solely on preferential questions such as comparing or ranking alternatives. This allows eliciting in principle arbitrarily flexible densities, but flow estimation is susceptible to the challenge of collapsing or diverging probability mass that makes it difficult in practice. We tackle this problem by introducing a novel functional prior for the flow, motivated by a decision-theoretic argument, and show empirically that the belief density can be inferred as the function-space maximum a posteriori estimate. We demonstrate our method by eliciting multivariate belief densities of simulated experts, including the prior belief of a general-purpose large language model over a real-world dataset.

Amortized Bayesian Workflow (Extended Abstract)

Bayesian inference often faces a trade-off between computational speed and sampling accuracy. We propose an adaptive workflow that integrates rapid amortized inference with gold-standard MCMC techniques to achieve both speed and accuracy when performing inference on many observed datasets. Our approach uses principled diagnostics to guide the choice of inference method for each dataset, moving along the Pareto front from fast amortized sampling to slower but guaranteed-accurate MCMC when necessary. By reusing computations across steps, our workflow creates synergies between amortized and MCMC-based inference. We demonstrate the effectiveness of this integrated approach on a generalized extreme value task with 1000 observed data sets, showing 90x time efficiency gains while maintaining high posterior quality.

Improving robustness to corruptions with multiplicative weight perturbations

Deep neural networks (DNNs) excel on clean images but struggle with corrupted ones. Incorporating specific corruptions into the data augmentation pipeline can improve robustness to those corruptions but may harm performance on clean images and other types of distortion. In this paper, we introduce an alternative approach that improves the robustness of DNNs to a wide range of corruptions without compromising accuracy on clean images. We first demonstrate that input perturbations can be mimicked by multiplicative perturbations in the weight space. Leveraging this, we propose Data Augmentation via Multiplicative Perturbation (DAMP), a training method that optimizes DNNs under random multiplicative weight perturbations. We also examine the recently proposed Adaptive Sharpness-Aware Minimization (ASAM) and show that it optimizes DNNs under adversarial multiplicative weight perturbations. Experiments on image classification datasets (CIFAR-10/100, TinyImageNet and ImageNet) and neural network architectures (ResNet50, ViT-S/16) show that DAMP enhances model generalization performance in the presence of corruptions across different settings. Notably, DAMP is able to train a ViT-S/16 on ImageNet from scratch, reaching the top-1 error of 23.7% which is comparable to ResNet50 without extensive data augmentations.