Amortized Bayesian Experimental Design for Decision-Making

Many critical decisions, such as personalized medical diagnoses and product pricing, are made based on insights gained from designing, observing, and analyzing a series of experiments. This highlights the crucial role of experimental design, which goes beyond merely collecting information on system parameters as in traditional Bayesian experimental design (BED), but also plays a key part in facilitating downstream decision-making. Most recent BED methods use an amortized policy network to rapidly design experiments. However, the information gathered through these methods is suboptimal for down-the-line decision-making, as the experiments are not inherently designed with downstream objectives in mind. In this paper, we present an amortized decision-aware BED framework that prioritizes maximizing downstream decision utility. We introduce a novel architecture, the Transformer Neural Decision Process (TNDP), capable of instantly proposing the next experimental design, whilst inferring the downstream decision, thus effectively amortizing both tasks within a unified workflow. We demonstrate the performance of our method across several tasks, showing that it can deliver informative designs and facilitate accurate decision-making.

Amortized Probabilistic Conditioning for Optimization, Simulation and Inference

Amortized meta-learning methods based on pre-training have propelled fields like natural language processing and vision. Transformer-based neural processes and their variants are leading models for probabilistic meta-learning with a tractable objective. Often trained on synthetic data, these models implicitly capture essential latent information in the data-generation process. However, existing methods do not allow users to flexibly inject (condition on) and extract (predict) this probabilistic latent information at runtime, which is key to many tasks. We introduce the Amortized Conditioning Engine (ACE), a new transformer-based meta-learning model that explicitly represents latent variables of interest. ACE affords conditioning on both observed data and interpretable latent variables, the inclusion of priors at runtime, and outputs predictive distributions for discrete and continuous data and latents. We show ACE's modeling flexibility and performance in diverse tasks such as image completion and classification, Bayesian optimization, and simulation-based inference.

Cost-aware Simulation-based Inference

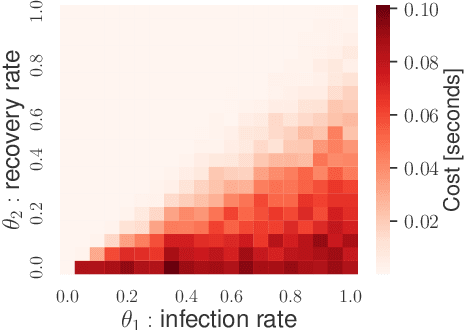
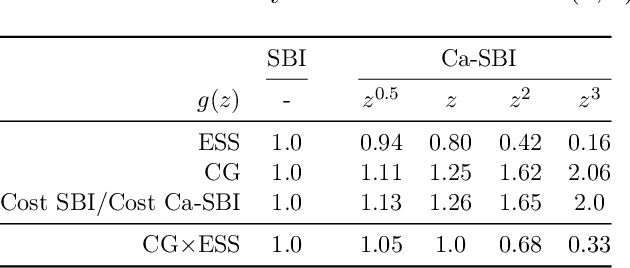
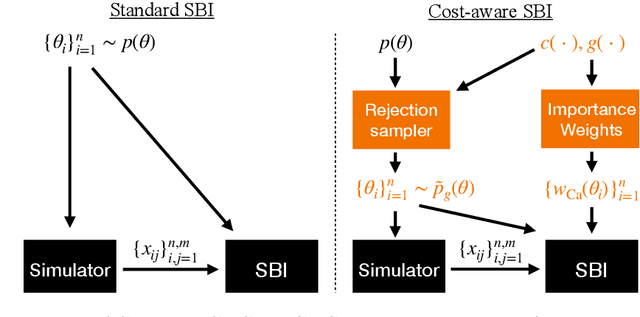
Simulation-based inference (SBI) is the preferred framework for estimating parameters of intractable models in science and engineering. A significant challenge in this context is the large computational cost of simulating data from complex models, and the fact that this cost often depends on parameter values. We therefore propose \textit{cost-aware SBI methods} which can significantly reduce the cost of existing sampling-based SBI methods, such as neural SBI and approximate Bayesian computation. This is achieved through a combination of rejection and self-normalised importance sampling, which significantly reduces the number of expensive simulations needed. Our approach is studied extensively on models from epidemiology to telecommunications engineering, where we obtain significant reductions in the overall cost of inference.

Practical Equivariances via Relational Conditional Neural Processes

Conditional Neural Processes (CNPs) are a class of metalearning models popular for combining the runtime efficiency of amortized inference with reliable uncertainty quantification. Many relevant machine learning tasks, such as spatio-temporal modeling, Bayesian Optimization and continuous control, contain equivariances -- for example to translation -- which the model can exploit for maximal performance. However, prior attempts to include equivariances in CNPs do not scale effectively beyond two input dimensions. In this work, we propose Relational Conditional Neural Processes (RCNPs), an effective approach to incorporate equivariances into any neural process model. Our proposed method extends the applicability and impact of equivariant neural processes to higher dimensions. We empirically demonstrate the competitive performance of RCNPs on a large array of tasks naturally containing equivariances.

Learning Robust Statistics for Simulation-based Inference under Model Misspecification

Simulation-based inference (SBI) methods such as approximate Bayesian computation (ABC), synthetic likelihood, and neural posterior estimation (NPE) rely on simulating statistics to infer parameters of intractable likelihood models. However, such methods are known to yield untrustworthy and misleading inference outcomes under model misspecification, thus hindering their widespread applicability. In this work, we propose the first general approach to handle model misspecification that works across different classes of SBI methods. Leveraging the fact that the choice of statistics determines the degree of misspecification in SBI, we introduce a regularized loss function that penalises those statistics that increase the mismatch between the data and the model. Taking NPE and ABC as use cases, we demonstrate the superior performance of our method on high-dimensional time-series models that are artificially misspecified. We also apply our method to real data from the field of radio propagation where the model is known to be misspecified. We show empirically that the method yields robust inference in misspecified scenarios, whilst still being accurate when the model is well-specified.

Bayesian Optimization Augmented with Actively Elicited Expert Knowledge

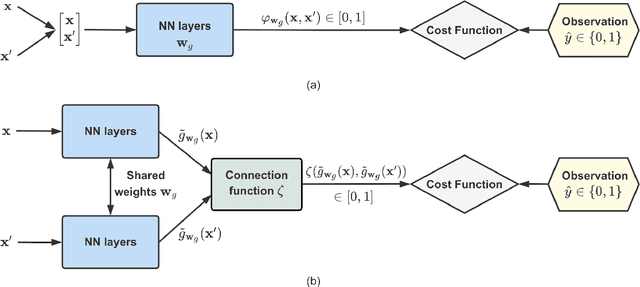
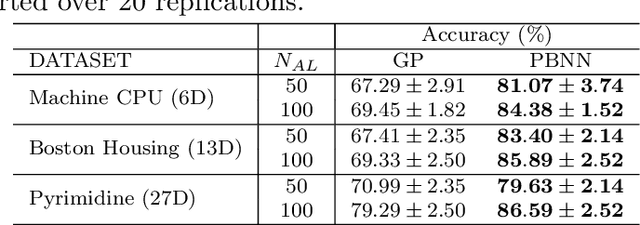
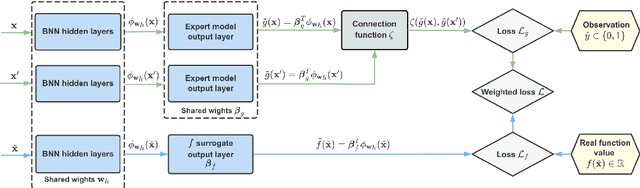
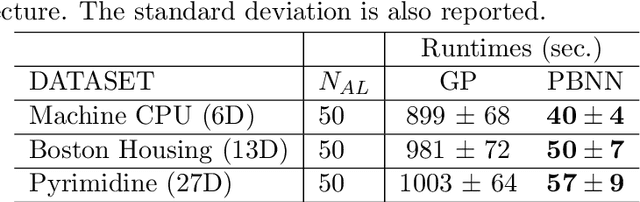
Bayesian optimization (BO) is a well-established method to optimize black-box functions whose direct evaluations are costly. In this paper, we tackle the problem of incorporating expert knowledge into BO, with the goal of further accelerating the optimization, which has received very little attention so far. We design a multi-task learning architecture for this task, with the goal of jointly eliciting the expert knowledge and minimizing the objective function. In particular, this allows for the expert knowledge to be transferred into the BO task. We introduce a specific architecture based on Siamese neural networks to handle the knowledge elicitation from pairwise queries. Experiments on various benchmark functions with both simulated and actual human experts show that the proposed method significantly speeds up BO even when the expert knowledge is biased compared to the objective function.