Embarrassingly Parallel GFlowNets

GFlowNets are a promising alternative to MCMC sampling for discrete compositional random variables. Training GFlowNets requires repeated evaluations of the unnormalized target distribution or reward function. However, for large-scale posterior sampling, this may be prohibitive since it incurs traversing the data several times. Moreover, if the data are distributed across clients, employing standard GFlowNets leads to intensive client-server communication. To alleviate both these issues, we propose embarrassingly parallel GFlowNet (EP-GFlowNet). EP-GFlowNet is a provably correct divide-and-conquer method to sample from product distributions of the form $R(\cdot) \propto R_1(\cdot) ... R_N(\cdot)$ -- e.g., in parallel or federated Bayes, where each $R_n$ is a local posterior defined on a data partition. First, in parallel, we train a local GFlowNet targeting each $R_n$ and send the resulting models to the server. Then, the server learns a global GFlowNet by enforcing our newly proposed \emph{aggregating balance} condition, requiring a single communication step. Importantly, EP-GFlowNets can also be applied to multi-objective optimization and model reuse. Our experiments illustrate the EP-GFlowNets's effectiveness on many tasks, including parallel Bayesian phylogenetics, multi-objective multiset, sequence generation, and federated Bayesian structure learning.

Learning Robust Statistics for Simulation-based Inference under Model Misspecification

Simulation-based inference (SBI) methods such as approximate Bayesian computation (ABC), synthetic likelihood, and neural posterior estimation (NPE) rely on simulating statistics to infer parameters of intractable likelihood models. However, such methods are known to yield untrustworthy and misleading inference outcomes under model misspecification, thus hindering their widespread applicability. In this work, we propose the first general approach to handle model misspecification that works across different classes of SBI methods. Leveraging the fact that the choice of statistics determines the degree of misspecification in SBI, we introduce a regularized loss function that penalises those statistics that increase the mismatch between the data and the model. Taking NPE and ABC as use cases, we demonstrate the superior performance of our method on high-dimensional time-series models that are artificially misspecified. We also apply our method to real data from the field of radio propagation where the model is known to be misspecified. We show empirically that the method yields robust inference in misspecified scenarios, whilst still being accurate when the model is well-specified.

Minimal Learning Machine for Multi-Label Learning

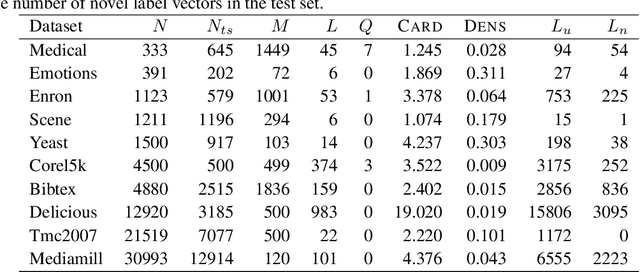
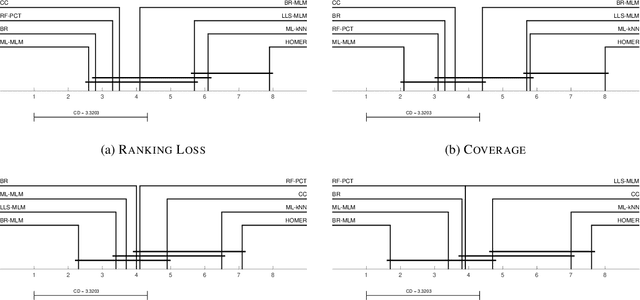
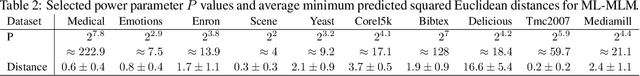
Distance-based supervised method, the minimal learning machine, constructs a predictive model from data by learning a mapping between input and output distance matrices. In this paper, we propose methods and evaluate how this technique and its core component, the distance mapping, can be adapted to multi-label learning. The proposed approach is based on combining the distance mapping with an inverse distance weighting. Although the proposal is one of the simplest methods in the multi-label learning literature, it achieves state-of-the-art performance for small to moderate-sized multi-label learning problems. Besides its simplicity, the proposed method is fully deterministic and its hyper-parameter can be selected via ranking loss-based statistic which has a closed form, thus avoiding conventional cross-validation-based hyper-parameter tuning. In addition, due to its simple linear distance mapping-based construction, we demonstrate that the proposed method can assess predictions' uncertainty for multi-label classification, which is a valuable capability for data-centric machine learning pipelines.

Distill n' Explain: explaining graph neural networks using simple surrogates

Explaining node predictions in graph neural networks (GNNs) often boils down to finding graph substructures that preserve predictions. Finding these structures usually implies back-propagating through the GNN, bonding the complexity (e.g., number of layers) of the GNN to the cost of explaining it. This naturally begs the question: Can we break this bond by explaining a simpler surrogate GNN? To answer the question, we propose Distill n' Explain (DnX). First, DnX learns a surrogate GNN via knowledge distillation. Then, DnX extracts node or edge-level explanations by solving a simple convex program. We also propose FastDnX, a faster version of DnX that leverages the linear decomposition of our surrogate model. Experiments show that DnX and FastDnX often outperform state-of-the-art GNN explainers while being orders of magnitude faster. Additionally, we support our empirical findings with theoretical results linking the quality of the surrogate model (i.e., distillation error) to the faithfulness of explanations.