Deep Random Features for Scalable Interpolation of Spatiotemporal Data

The rapid growth of earth observation systems calls for a scalable approach to interpolate remote-sensing observations. These methods in principle, should acquire more information about the observed field as data grows. Gaussian processes (GPs) are candidate model choices for interpolation. However, due to their poor scalability, they usually rely on inducing points for inference, which restricts their expressivity. Moreover, commonly imposed assumptions such as stationarity prevents them from capturing complex patterns in the data. While deep GPs can overcome this issue, training and making inference with them are difficult, again requiring crude approximations via inducing points. In this work, we instead approach the problem through Bayesian deep learning, where spatiotemporal fields are represented by deep neural networks, whose layers share the inductive bias of stationary GPs on the plane/sphere via random feature expansions. This allows one to (1) capture high frequency patterns in the data, and (2) use mini-batched gradient descent for large scale training. We experiment on various remote sensing data at local/global scales, showing that our approach produce competitive or superior results to existing methods, with well-calibrated uncertainties.

Scalable Data Assimilation with Message Passing

Data assimilation is a core component of numerical weather prediction systems. The large quantity of data processed during assimilation requires the computation to be distributed across increasingly many compute nodes, yet existing approaches suffer from synchronisation overhead in this setting. In this paper, we exploit the formulation of data assimilation as a Bayesian inference problem and apply a message-passing algorithm to solve the spatial inference problem. Since message passing is inherently based on local computations, this approach lends itself to parallel and distributed computation. In combination with a GPU-accelerated implementation, we can scale the algorithm to very large grid sizes while retaining good accuracy and compute and memory requirements.

Iterated INLA for State and Parameter Estimation in Nonlinear Dynamical Systems

Data assimilation (DA) methods use priors arising from differential equations to robustly interpolate and extrapolate data. Popular techniques such as ensemble methods that handle high-dimensional, nonlinear PDE priors focus mostly on state estimation, however can have difficulty learning the parameters accurately. On the other hand, machine learning based approaches can naturally learn the state and parameters, but their applicability can be limited, or produce uncertainties that are hard to interpret. Inspired by the Integrated Nested Laplace Approximation (INLA) method in spatial statistics, we propose an alternative approach to DA based on iteratively linearising the dynamical model. This produces a Gaussian Markov random field at each iteration, enabling one to use INLA to infer the state and parameters. Our approach can be used for arbitrary nonlinear systems, while retaining interpretability, and is furthermore demonstrated to outperform existing methods on the DA task. By providing a more nuanced approach to handling nonlinear PDE priors, our methodology offers improved accuracy and robustness in predictions, especially where data sparsity is prevalent.

Gaussian Processes on Cellular Complexes

In recent years, there has been considerable interest in developing machine learning models on graphs in order to account for topological inductive biases. In particular, recent attention was given to Gaussian processes on such structures since they can additionally account for uncertainty. However, graphs are limited to modelling relations between two vertices. In this paper, we go beyond this dyadic setting and consider polyadic relations that include interactions between vertices, edges and one of their generalisations, known as cells. Specifically, we propose Gaussian processes on cellular complexes, a generalisation of graphs that captures interactions between these higher-order cells. One of our key contributions is the derivation of two novel kernels, one that generalises the graph Mat\'ern kernel and one that additionally mixes information of different cell types.

Actually Sparse Variational Gaussian Processes

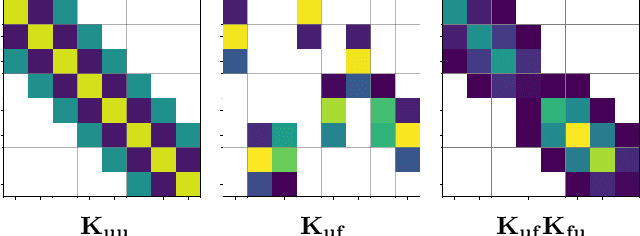
Gaussian processes (GPs) are typically criticised for their unfavourable scaling in both computational and memory requirements. For large datasets, sparse GPs reduce these demands by conditioning on a small set of inducing variables designed to summarise the data. In practice however, for large datasets requiring many inducing variables, such as low-lengthscale spatial data, even sparse GPs can become computationally expensive, limited by the number of inducing variables one can use. In this work, we propose a new class of inter-domain variational GP, constructed by projecting a GP onto a set of compactly supported B-spline basis functions. The key benefit of our approach is that the compact support of the B-spline basis functions admits the use of sparse linear algebra to significantly speed up matrix operations and drastically reduce the memory footprint. This allows us to very efficiently model fast-varying spatial phenomena with tens of thousands of inducing variables, where previous approaches failed.

Short-term Prediction and Filtering of Solar Power Using State-Space Gaussian Processes

Short-term forecasting of solar photovoltaic energy (PV) production is important for powerplant management. Ideally these forecasts are equipped with error bars, so that downstream decisions can account for uncertainty. To produce predictions with error bars in this setting, we consider Gaussian processes (GPs) for modelling and predicting solar photovoltaic energy production in the UK. A standard application of GP regression on the PV timeseries data is infeasible due to the large data size and non-Gaussianity of PV readings. However, this is made possible by leveraging recent advances in scalable GP inference, in particular, by using the state-space form of GPs, combined with modern variational inference techniques. The resulting model is not only scalable to large datasets but can also handle continuous data streams via Kalman filtering.

Vector-valued Gaussian Processes on Riemannian Manifolds via Gauge Independent Projected Kernels

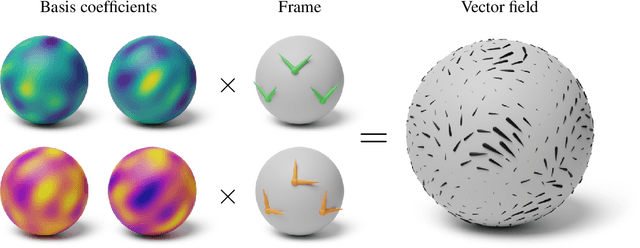
Gaussian processes are machine learning models capable of learning unknown functions in a way that represents uncertainty, thereby facilitating construction of optimal decision-making systems. Motivated by a desire to deploy Gaussian processes in novel areas of science, a rapidly-growing line of research has focused on constructively extending these models to handle non-Euclidean domains, including Riemannian manifolds, such as spheres and tori. We propose techniques that generalize this class to model vector fields on Riemannian manifolds, which are important in a number of application areas in the physical sciences. To do so, we present a general recipe for constructing gauge independent kernels, which induce Gaussian vector fields, i.e. vector-valued Gaussian processes coherent with geometry, from scalar-valued Riemannian kernels. We extend standard Gaussian process training methods, such as variational inference, to this setting. This enables vector-valued Gaussian processes on Riemannian manifolds to be trained using standard methods and makes them accessible to machine learning practitioners.

A Unifying and Canonical Description of Measure-Preserving Diffusions

A complete recipe of measure-preserving diffusions in Euclidean space was recently derived unifying several MCMC algorithms into a single framework. In this paper, we develop a geometric theory that improves and generalises this construction to any manifold. We thereby demonstrate that the completeness result is a direct consequence of the topology of the underlying manifold and the geometry induced by the target measure $P$; there is no need to introduce other structures such as a Riemannian metric, local coordinates, or a reference measure. Instead, our framework relies on the intrinsic geometry of $P$ and in particular its canonical derivative, the deRham rotationnel, which allows us to parametrise the Fokker--Planck currents of measure-preserving diffusions using potentials. The geometric formalism can easily incorporate constraints and symmetries, and deliver new important insights, for example, a new complete recipe of Langevin-like diffusions that are suited to the construction of samplers. We also analyse the reversibility and dissipative properties of the diffusions, the associated deterministic flow on the space of measures, and the geometry of Langevin processes. Our article connects ideas from various literature and frames the theory of measure-preserving diffusions in its appropriate mathematical context.