Deep Learning as Ricci Flow

Deep neural networks (DNNs) are powerful tools for approximating the distribution of complex data. It is known that data passing through a trained DNN classifier undergoes a series of geometric and topological simplifications. While some progress has been made toward understanding these transformations in neural networks with smooth activation functions, an understanding in the more general setting of non-smooth activation functions, such as the rectified linear unit (ReLU), which tend to perform better, is required. Here we propose that the geometric transformations performed by DNNs during classification tasks have parallels to those expected under Hamilton's Ricci flow - a tool from differential geometry that evolves a manifold by smoothing its curvature, in order to identify its topology. To illustrate this idea, we present a computational framework to quantify the geometric changes that occur as data passes through successive layers of a DNN, and use this framework to motivate a notion of `global Ricci network flow' that can be used to assess a DNN's ability to disentangle complex data geometries to solve classification problems. By training more than $1,500$ DNN classifiers of different widths and depths on synthetic and real-world data, we show that the strength of global Ricci network flow-like behaviour correlates with accuracy for well-trained DNNs, independently of depth, width and data set. Our findings motivate the use of tools from differential and discrete geometry to the problem of explainability in deep learning.

Improving embedding of graphs with missing data by soft manifolds

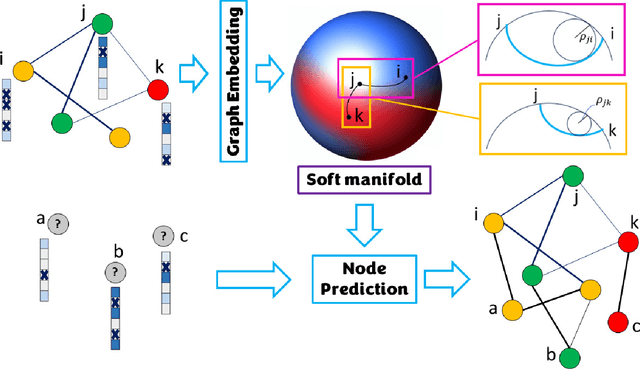
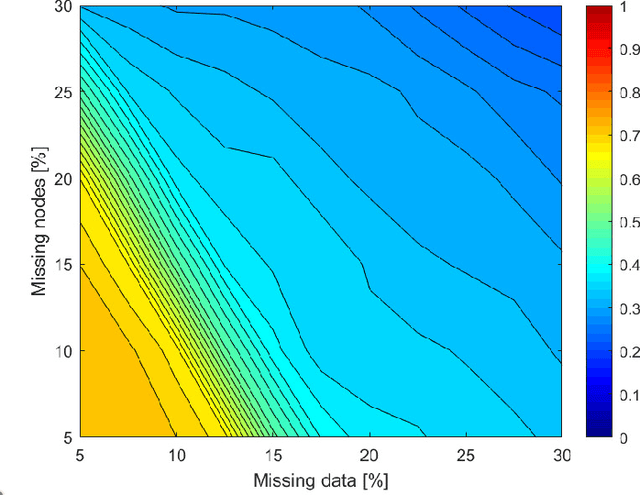
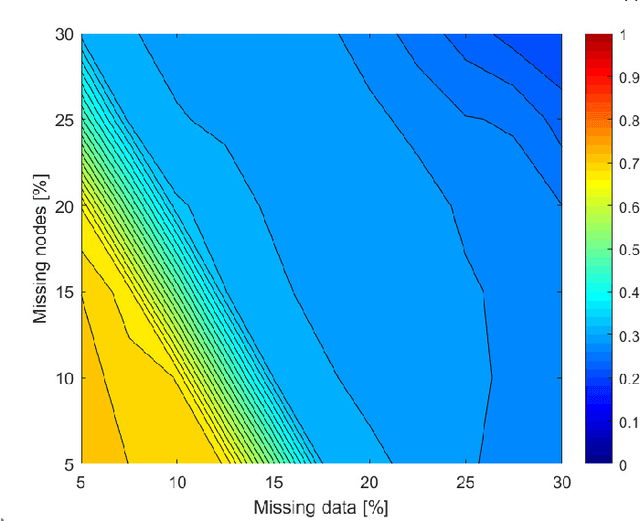
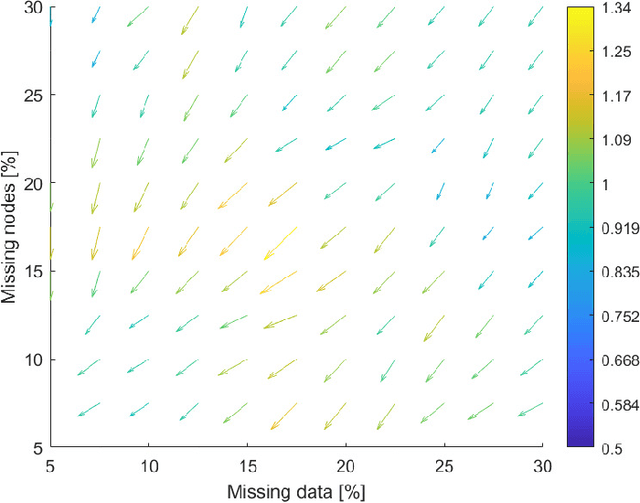
Embedding graphs in continous spaces is a key factor in designing and developing algorithms for automatic information extraction to be applied in diverse tasks (e.g., learning, inferring, predicting). The reliability of graph embeddings directly depends on how much the geometry of the continuous space matches the graph structure. Manifolds are mathematical structure that can enable to incorporate in their topological spaces the graph characteristics, and in particular nodes distances. State-of-the-art of manifold-based graph embedding algorithms take advantage of the assumption that the projection on a tangential space of each point in the manifold (corresponding to a node in the graph) would locally resemble a Euclidean space. Although this condition helps in achieving efficient analytical solutions to the embedding problem, it does not represent an adequate set-up to work with modern real life graphs, that are characterized by weighted connections across nodes often computed over sparse datasets with missing records. In this work, we introduce a new class of manifold, named soft manifold, that can solve this situation. In particular, soft manifolds are mathematical structures with spherical symmetry where the tangent spaces to each point are hypocycloids whose shape is defined according to the velocity of information propagation across the data points. Using soft manifolds for graph embedding, we can provide continuous spaces to pursue any task in data analysis over complex datasets. Experimental results on reconstruction tasks on synthetic and real datasets show how the proposed approach enable more accurate and reliable characterization of graphs in continuous spaces with respect to the state-of-the-art.

Warped geometric information on the optimisation of Euclidean functions

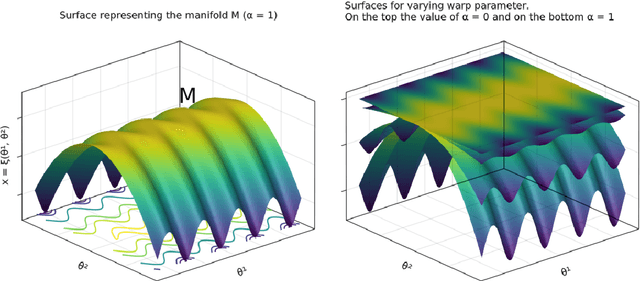
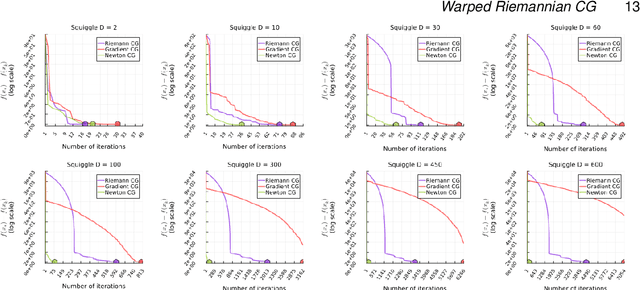
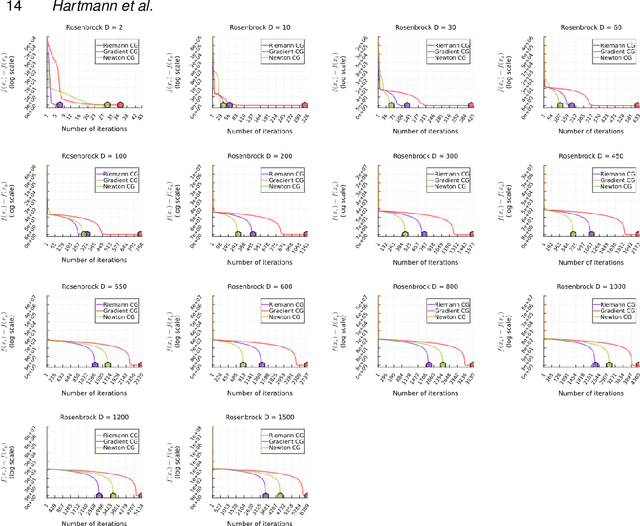
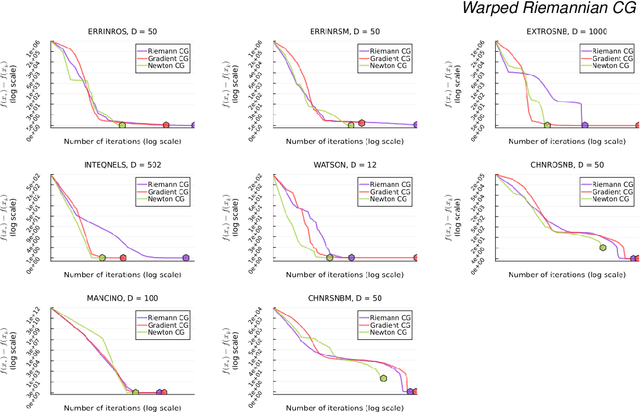
We consider the fundamental task of optimizing a real-valued function defined in a potentially high-dimensional Euclidean space, such as the loss function in many machine-learning tasks or the logarithm of the probability distribution in statistical inference. We use the warped Riemannian geometry notions to redefine the optimisation problem of a function on Euclidean space to a Riemannian manifold with a warped metric, and then find the function's optimum along this manifold. The warped metric chosen for the search domain induces a computational friendly metric-tensor for which optimal search directions associate with geodesic curves on the manifold becomes easier to compute. Performing optimization along geodesics is known to be generally infeasible, yet we show that in this specific manifold we can analytically derive Taylor approximations up to third-order. In general these approximations to the geodesic curve will not lie on the manifold, however we construct suitable retraction maps to pull them back onto the manifold. Therefore, we can efficiently optimize along the approximate geodesic curves. We cover the related theory, describe a practical optimization algorithm and empirically evaluate it on a collection of challenging optimisation benchmarks. Our proposed algorithm, using third-order approximation of geodesics, outperforms standard Euclidean gradient-based counterparts in term of number of iterations until convergence and an alternative method for Hessian-based optimisation routines.

Targeted Separation and Convergence with Kernel Discrepancies

Maximum mean discrepancies (MMDs) like the kernel Stein discrepancy (KSD) have grown central to a wide range of applications, including hypothesis testing, sampler selection, distribution approximation, and variational inference. In each setting, these kernel-based discrepancy measures are required to (i) separate a target P from other probability measures or even (ii) control weak convergence to P. In this article we derive new sufficient and necessary conditions to ensure (i) and (ii). For MMDs on separable metric spaces, we characterize those kernels that separate Bochner embeddable measures and introduce simple conditions for separating all measures with unbounded kernels and for controlling convergence with bounded kernels. We use these results on $\mathbb{R}^d$ to substantially broaden the known conditions for KSD separation and convergence control and to develop the first KSDs known to exactly metrize weak convergence to P. Along the way, we highlight the implications of our results for hypothesis testing, measuring and improving sample quality, and sampling with Stein variational gradient descent.

Geometric Methods for Sampling, Optimisation, Inference and Adaptive Agents

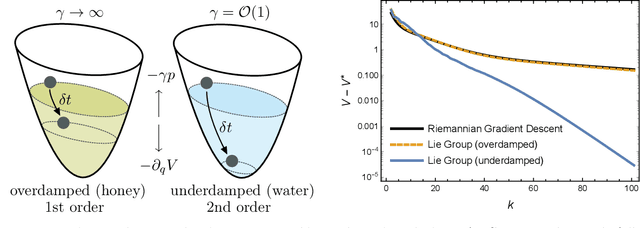
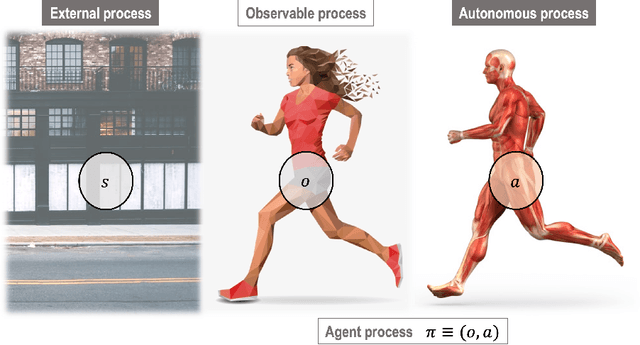
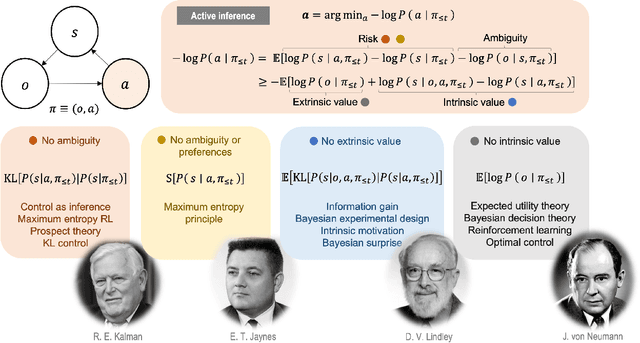
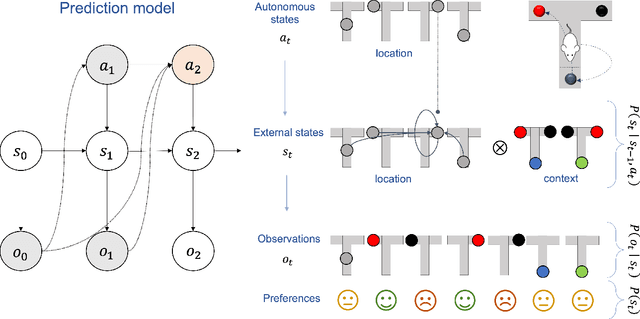
In this chapter, we identify fundamental geometric structures that underlie the problems of sampling, optimisation, inference and adaptive decision-making. Based on this identification, we derive algorithms that exploit these geometric structures to solve these problems efficiently. We show that a wide range of geometric theories emerge naturally in these fields, ranging from measure-preserving processes, information divergences, Poisson geometry, and geometric integration. Specifically, we explain how \emph{(i)} leveraging the symplectic geometry of Hamiltonian systems enable us to construct (accelerated) sampling and optimisation methods, \emph{(ii)} the theory of Hilbertian subspaces and Stein operators provides a general methodology to obtain robust estimators, \emph{(iii)} preserving the information geometry of decision-making yields adaptive agents that perform active inference. Throughout, we emphasise the rich connections between these fields; e.g., inference draws on sampling and optimisation, and adaptive decision-making assesses decisions by inferring their counterfactual consequences. Our exposition provides a conceptual overview of underlying ideas, rather than a technical discussion, which can be found in the references herein.

Optimization on manifolds: A symplectic approach

There has been great interest in using tools from dynamical systems and numerical analysis of differential equations to understand and construct new optimization methods. In particular, recently a new paradigm has emerged that applies ideas from mechanics and geometric integration to obtain accelerated optimization methods on Euclidean spaces. This has important consequences given that accelerated methods are the workhorses behind many machine learning applications. In this paper we build upon these advances and propose a framework for dissipative and constrained Hamiltonian systems that is suitable for solving optimization problems on arbitrary smooth manifolds. Importantly, this allows us to leverage the well-established theory of symplectic integration to derive "rate-matching" dissipative integrators. This brings a new perspective to optimization on manifolds whereby convergence guarantees follow by construction from classical arguments in symplectic geometry and backward error analysis. Moreover, we construct two dissipative generalizations of leapfrog that are straightforward to implement: one for Lie groups and homogeneous spaces, that relies on the tractable geodesic flow or a retraction thereof, and the other for constrained submanifolds that is based on a dissipative generalization of the famous RATTLE integrator.

A Unifying and Canonical Description of Measure-Preserving Diffusions

A complete recipe of measure-preserving diffusions in Euclidean space was recently derived unifying several MCMC algorithms into a single framework. In this paper, we develop a geometric theory that improves and generalises this construction to any manifold. We thereby demonstrate that the completeness result is a direct consequence of the topology of the underlying manifold and the geometry induced by the target measure $P$; there is no need to introduce other structures such as a Riemannian metric, local coordinates, or a reference measure. Instead, our framework relies on the intrinsic geometry of $P$ and in particular its canonical derivative, the deRham rotationnel, which allows us to parametrise the Fokker--Planck currents of measure-preserving diffusions using potentials. The geometric formalism can easily incorporate constraints and symmetries, and deliver new important insights, for example, a new complete recipe of Langevin-like diffusions that are suited to the construction of samplers. We also analyse the reversibility and dissipative properties of the diffusions, the associated deterministic flow on the space of measures, and the geometry of Langevin processes. Our article connects ideas from various literature and frames the theory of measure-preserving diffusions in its appropriate mathematical context.

Metrizing Weak Convergence with Maximum Mean Discrepancies

Theorem 12 of Simon-Gabriel & Sch\"olkopf (JMLR, 2018) seemed to close a 40-year-old quest to characterize maximum mean discrepancies (MMD) that metrize the weak convergence of probability measures. We prove, however, that the theorem is incorrect and provide a correction. We show that, on a locally compact, non-compact, Hausdorff space, the MMD of a bounded continuous Borel measurable kernel k, whose RKHS-functions vanish at infinity, metrizes the weak convergence of probability measures if and only if k is continuous and integrally strictly positive definite (ISPD) over all signed, finite, regular Borel measures. We also show that, contrary to the claim of the aforementioned Theorem 12, there exist both bounded continuous ISPD kernels that do not metrize weak convergence and bounded continuous non-ISPD kernels that do metrize it.

Minimum Stein Discrepancy Estimators

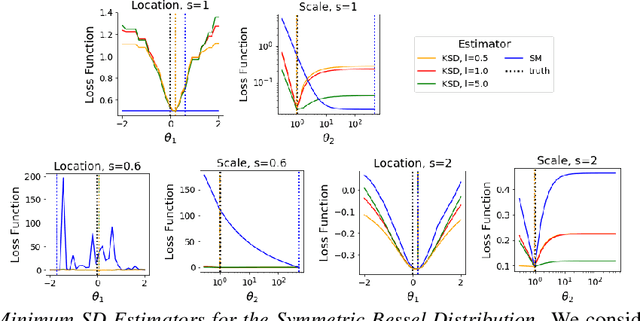
When maximum likelihood estimation is infeasible, one often turns to score matching, contrastive divergence, or minimum probability flow learning to obtain tractable parameter estimates. We provide a unifying perspective of these techniques as minimum Stein discrepancy estimators and use this lens to design new diffusion kernel Stein discrepancy (DKSD) and diffusion score matching (DSM) estimators with complementary strengths. We establish the consistency, asymptotic normality, and robustness of DKSD and DSM estimators, derive stochastic Riemannian gradient descent algorithms for their efficient optimization, and demonstrate their advantages over score matching in models with non-smooth densities or heavy tailed distributions.

Statistical Inference for Generative Models with Maximum Mean Discrepancy

While likelihood-based inference and its variants provide a statistically efficient and widely applicable approach to parametric inference, their application to models involving intractable likelihoods poses challenges. In this work, we study a class of minimum distance estimators for intractable generative models, that is, statistical models for which the likelihood is intractable, but simulation is cheap. The distance considered, maximum mean discrepancy (MMD), is defined through the embedding of probability measures into a reproducing kernel Hilbert space. We study the theoretical properties of these estimators, showing that they are consistent, asymptotically normal and robust to model misspecification. A main advantage of these estimators is the flexibility offered by the choice of kernel, which can be used to trade-off statistical efficiency and robustness. On the algorithmic side, we study the geometry induced by MMD on the parameter space and use this to introduce a novel natural gradient descent-like algorithm for efficient implementation of these estimators. We illustrate the relevance of our theoretical results on several classes of models including a discrete-time latent Markov process and two multivariate stochastic differential equation models.