Geometric Methods for Sampling, Optimisation, Inference and Adaptive Agents

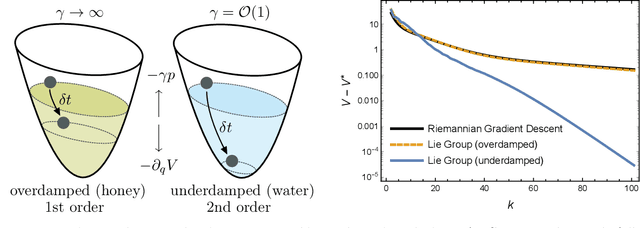
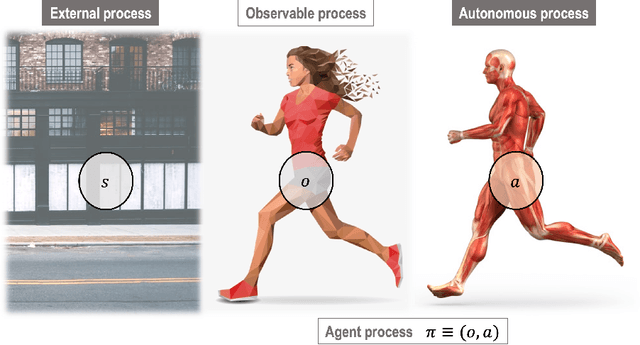
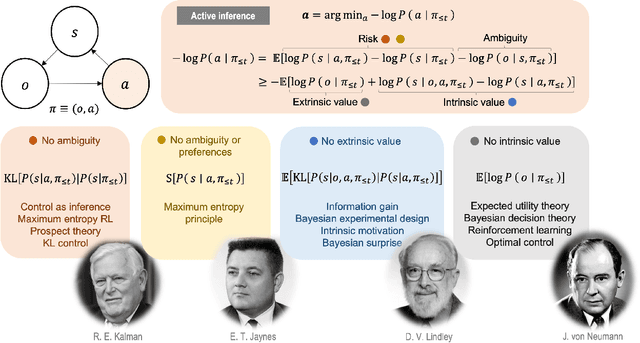
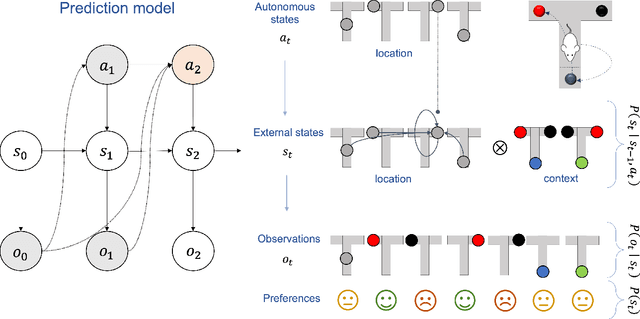
In this chapter, we identify fundamental geometric structures that underlie the problems of sampling, optimisation, inference and adaptive decision-making. Based on this identification, we derive algorithms that exploit these geometric structures to solve these problems efficiently. We show that a wide range of geometric theories emerge naturally in these fields, ranging from measure-preserving processes, information divergences, Poisson geometry, and geometric integration. Specifically, we explain how \emph{(i)} leveraging the symplectic geometry of Hamiltonian systems enable us to construct (accelerated) sampling and optimisation methods, \emph{(ii)} the theory of Hilbertian subspaces and Stein operators provides a general methodology to obtain robust estimators, \emph{(iii)} preserving the information geometry of decision-making yields adaptive agents that perform active inference. Throughout, we emphasise the rich connections between these fields; e.g., inference draws on sampling and optimisation, and adaptive decision-making assesses decisions by inferring their counterfactual consequences. Our exposition provides a conceptual overview of underlying ideas, rather than a technical discussion, which can be found in the references herein.

Optimization on manifolds: A symplectic approach

There has been great interest in using tools from dynamical systems and numerical analysis of differential equations to understand and construct new optimization methods. In particular, recently a new paradigm has emerged that applies ideas from mechanics and geometric integration to obtain accelerated optimization methods on Euclidean spaces. This has important consequences given that accelerated methods are the workhorses behind many machine learning applications. In this paper we build upon these advances and propose a framework for dissipative and constrained Hamiltonian systems that is suitable for solving optimization problems on arbitrary smooth manifolds. Importantly, this allows us to leverage the well-established theory of symplectic integration to derive "rate-matching" dissipative integrators. This brings a new perspective to optimization on manifolds whereby convergence guarantees follow by construction from classical arguments in symplectic geometry and backward error analysis. Moreover, we construct two dissipative generalizations of leapfrog that are straightforward to implement: one for Lie groups and homogeneous spaces, that relies on the tractable geodesic flow or a retraction thereof, and the other for constrained submanifolds that is based on a dissipative generalization of the famous RATTLE integrator.

Distributed Optimization, Averaging via ADMM, and Network Topology

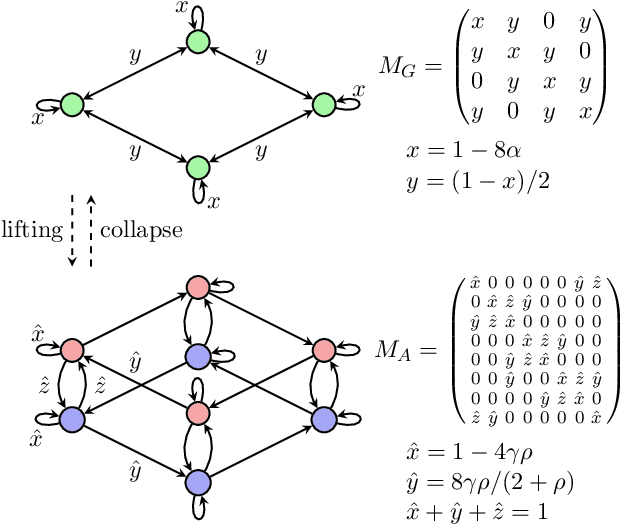
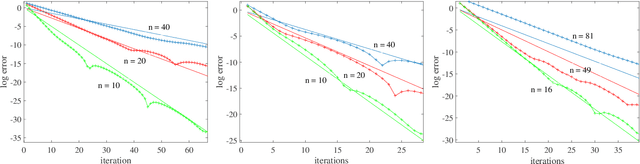
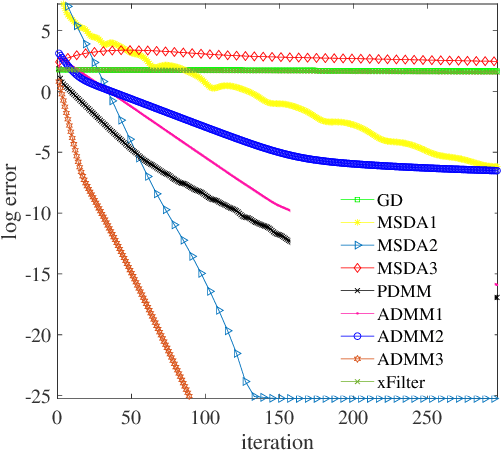
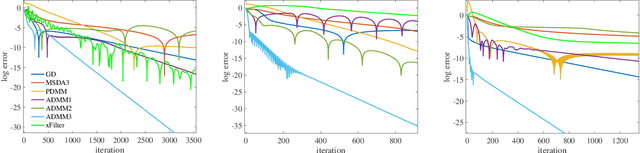
There has been an increasing necessity for scalable optimization methods, especially due to the explosion in the size of datasets and model complexity in modern machine learning applications. Scalable solvers often distribute the computation over a network of processing units. For simple algorithms such as gradient descent the dependency of the convergence time with the topology of this network is well-known. However, for more involved algorithms such as the Alternating Direction Methods of Multipliers (ADMM) much less is known. At the heart of many distributed optimization algorithms there exists a gossip subroutine which averages local information over the network, and whose efficiency is crucial for the overall performance of the method. In this paper we review recent research in this area and, with the goal of isolating such a communication exchange behaviour, we compare different algorithms when applied to a canonical distributed averaging consensus problem. We also show interesting connections between ADMM and lifted Markov chains besides providing an explicitly characterization of its convergence and optimal parameter tuning in terms of spectral properties of the network. Finally, we empirically study the connection between network topology and convergence rates for different algorithms on a real world problem of sensor localization.

On Dissipative Symplectic Integration with Applications to Gradient-Based Optimization

Continuous-time dynamical systems have proved useful in providing conceptual and quantitative insights into gradient-based optimization. An important question that arises in this line of work is how to discretize the continuous-time system in such a way that its stability and rates of convergence are preserved. In this paper we propose a geometric framework in which such discretizations can be realized systematically, enabling the derivation of rate-matching optimization algorithms without the need for a discrete-time convergence analysis. More specifically, we show that a generalization of symplectic integrators to dissipative Hamiltonian systems is able to preserve continuous-time rates of convergence up to a controlled error. Our arguments rely on a combination of backward-error analysis with fundamental results from symplectic geometry.

Gradient Flows and Accelerated Proximal Splitting Methods

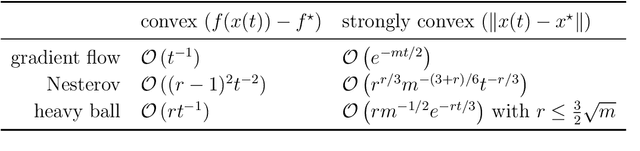
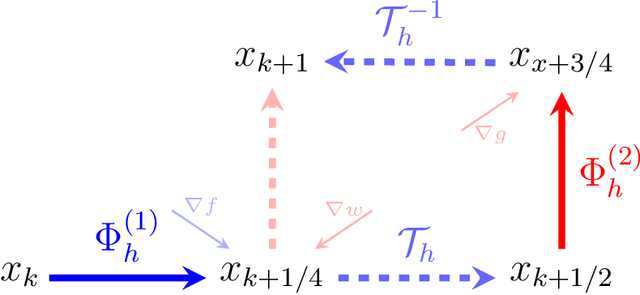
Proximal based algorithms are well-suited to nonsmooth optimization problems with important applications in signal processing, control theory, statistics and machine learning. There are essentially four basic types of proximal algorithms based on fixed-point iteration currently known: forward-backward splitting, forward-backward-forward or Tseng splitting, Douglas-Rachford, and the very recent Davis-Yin three-operator splitting. In addition, the alternating direction method of multipliers (ADMM) is also closely related. In this paper, we show that all these different methods can be derived from the gradient flow by using splitting methods for ordinary differential equations. Furthermore, applying similar discretization scheme to a particular second order differential equation results in accelerated variants of the respective algorithm, which can be of Nesterov or heavy ball type, although we treat both simultaneously. Many of the optimization algorithms we derive are new. For instance, we propose accelerated variants of Davis-Yin and two extensions of ADMM together with their accelerated variants. Interestingly, we show that (accelerated) ADMM corresponds to a rebalanced splitting which is a recent technique designed to preserve steady states of the differential equation. Overall, our results strengthen the connections between optimization and continuous dynamical systems and offer a more unified perspective on accelerated methods.

Conformal Symplectic and Relativistic Optimization

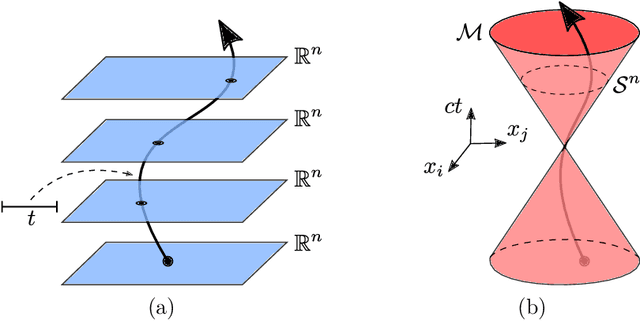
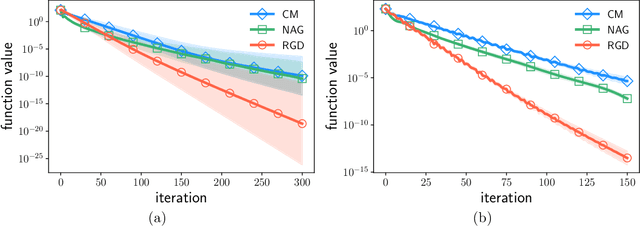
Although momentum-based optimization methods have had a remarkable impact on machine learning, their heuristic construction has been an obstacle to a deeper understanding. A promising direction to study these accelerated algorithms has been emerging through connections with continuous dynamical systems. Yet, it is unclear whether the main properties of the underlying dynamical system are preserved by the algorithms from which they are derived. Conformal Hamiltonian systems form a special class of dissipative systems, having a distinct symplectic geometry. In this paper, we show that gradient descent with momentum preserves this symplectic structure, while Nesterov's accelerated gradient method does not. More importantly, we propose a generalization of classical momentum based on the special theory of relativity. The resulting conformal symplectic and relativistic algorithm enjoys better stability since it operates on a different space compared to its classical predecessor. Its benefits are discussed and verified in deep learning experiments.

Kernel k-Groups via Hartigan's Method

Energy statistics was proposed by Sz\'{e}kely in the 80's inspired by Newton's gravitational potential in classical mechanics, and it provides a model-free hypothesis test for equality of distributions. In its original form, energy statistics was formulated in Euclidean spaces. More recently, it was generalized to metric spaces of negative type. In this paper, we consider a formulation for the clustering problem using a weighted version of energy statistics in spaces of negative type. We show that this approach leads to a quadratically constrained quadratic program in the associated kernel space, establishing connections with graph partitioning problems and kernel methods in unsupervised machine learning. To find local solutions of such an optimization problem, we propose an extension of Hartigan's method to kernel spaces. Our method has the same computational cost as kernel k-means algorithm, which is based on Lloyd's heuristic, but our numerical results show an improved performance, especially in high dimensions.

Relax, and Accelerate: A Continuous Perspective on ADMM

The acceleration technique first introduced by Nesterov for gradient descent is widely used in many machine learning applications, however it is not yet well-understood. Recently, significant progress has been made to close this understanding gap by using a continuous-time dynamical system perspective associated with gradient-based methods. In this paper, we extend this perspective by considering the continuous limit of the family of relaxed Alternating Direction Method of Multipliers (ADMM). We also introduce two new families of relaxed and accelerated ADMM algorithms, one follows Nesterov's acceleration approach and the other is inspired by Polyak's Heavy Ball method, and derive the continuous limit of these families of relaxed and accelerated algorithms as differential equations. Then, using a Lyapunov stability analysis of the dynamical systems, we obtain rate-of-convergence results for convex and strongly convex objective functions.

Tuning Over-Relaxed ADMM

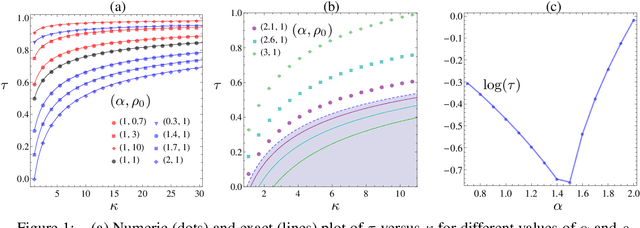
The framework of Integral Quadratic Constraints (IQC) reduces the computation of upper bounds on the convergence rate of several optimization algorithms to a semi-definite program (SDP). In the case of over-relaxed Alternating Direction Method of Multipliers (ADMM), an explicit and closed form solution to this SDP was derived in our recent work [1]. The purpose of this paper is twofold. First, we summarize these results. Second, we explore one of its consequences which allows us to obtain general and simple formulas for optimal parameter selection. These results are valid for arbitrary strongly convex objective functions.

An Explicit Rate Bound for the Over-Relaxed ADMM

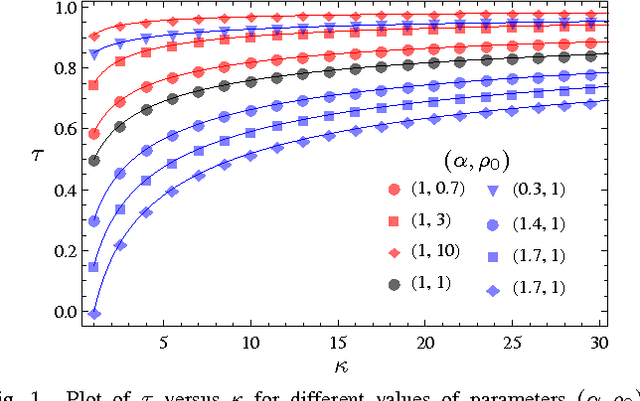
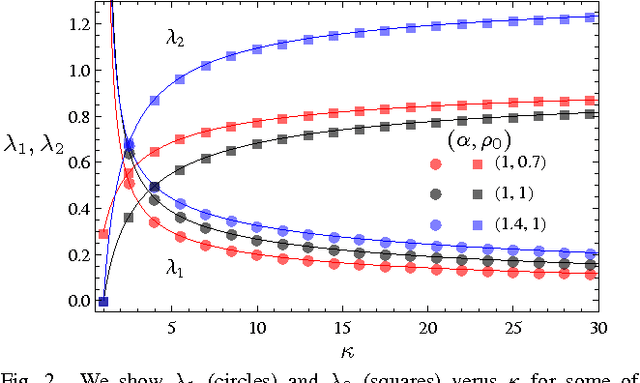
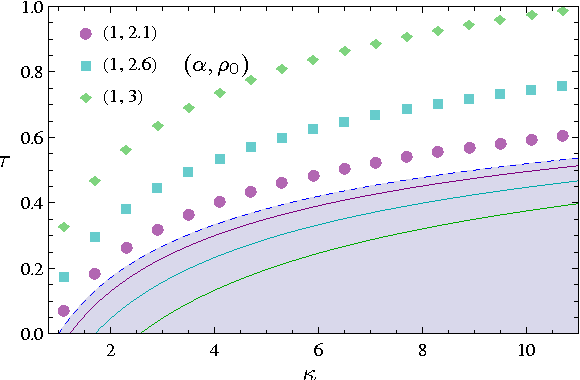
The framework of Integral Quadratic Constraints of Lessard et al. (2014) reduces the computation of upper bounds on the convergence rate of several optimization algorithms to semi-definite programming (SDP). Followup work by Nishihara et al. (2015) applies this technique to the entire family of over-relaxed Alternating Direction Method of Multipliers (ADMM). Unfortunately, they only provide an explicit error bound for sufficiently large values of some of the parameters of the problem, leaving the computation for the general case as a numerical optimization problem. In this paper we provide an exact analytical solution to this SDP and obtain a general and explicit upper bound on the convergence rate of the entire family of over-relaxed ADMM. Furthermore, we demonstrate that it is not possible to extract from this SDP a general bound better than ours. We end with a few numerical illustrations of our result and a comparison between the convergence rate we obtain for the ADMM with known convergence rates for the Gradient Descent.