Conformal Symplectic and Relativistic Optimization

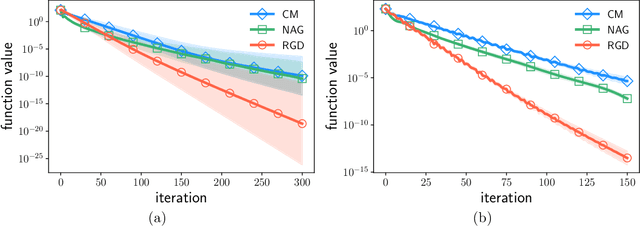
Although momentum-based optimization methods have had a remarkable impact on machine learning, their heuristic construction has been an obstacle to a deeper understanding. A promising direction to study these accelerated algorithms has been emerging through connections with continuous dynamical systems. Yet, it is unclear whether the main properties of the underlying dynamical system are preserved by the algorithms from which they are derived. Conformal Hamiltonian systems form a special class of dissipative systems, having a distinct symplectic geometry. In this paper, we show that gradient descent with momentum preserves this symplectic structure, while Nesterov's accelerated gradient method does not. More importantly, we propose a generalization of classical momentum based on the special theory of relativity. The resulting conformal symplectic and relativistic algorithm enjoys better stability since it operates on a different space compared to its classical predecessor. Its benefits are discussed and verified in deep learning experiments.