Automatic Joint Structured Pruning and Quantization for Efficient Neural Network Training and Compression

Structured pruning and quantization are fundamental techniques used to reduce the size of deep neural networks (DNNs) and typically are applied independently. Applying these techniques jointly via co-optimization has the potential to produce smaller, high-quality models. However, existing joint schemes are not widely used because of (1) engineering difficulties (complicated multi-stage processes), (2) black-box optimization (extensive hyperparameter tuning to control the overall compression), and (3) insufficient architecture generalization. To address these limitations, we present the framework GETA, which automatically and efficiently performs joint structured pruning and quantization-aware training on any DNNs. GETA introduces three key innovations: (i) a quantization-aware dependency graph (QADG) that constructs a pruning search space for generic quantization-aware DNN, (ii) a partially projected stochastic gradient method that guarantees layerwise bit constraints are satisfied, and (iii) a new joint learning strategy that incorporates interpretable relationships between pruning and quantization. We present numerical experiments on both convolutional neural networks and transformer architectures that show that our approach achieves competitive (often superior) performance compared to existing joint pruning and quantization methods.

Using Synthetic Data to Mitigate Unfairness and Preserve Privacy through Single-Shot Federated Learning

To address unfairness issues in federated learning (FL), contemporary approaches typically use frequent model parameter updates and transmissions between the clients and server. In such a process, client-specific information (e.g., local dataset size or data-related fairness metrics) must be sent to the server to compute, e.g., aggregation weights. All of this results in high transmission costs and the potential leakage of client information. As an alternative, we propose a strategy that promotes fair predictions across clients without the need to pass information between the clients and server iteratively and prevents client data leakage. For each client, we first use their local dataset to obtain a synthetic dataset by solving a bilevel optimization problem that addresses unfairness concerns during the learning process. We then pass each client's synthetic dataset to the server, the collection of which is used to train the server model using conventional machine learning techniques (that do not take fairness metrics into account). Thus, we eliminate the need to handle fairness-specific aggregation weights while preserving client privacy. Our approach requires only a single communication between the clients and the server, thus making it computationally cost-effective, able to maintain privacy, and able to ensuring fairness. We present empirical evidence to demonstrate the advantages of our approach. The results illustrate that our method effectively uses synthetic data as a means to mitigate unfairness and preserve client privacy.

A Stochastic-Gradient-based Interior-Point Algorithm for Solving Smooth Bound-Constrained Optimization Problems

A stochastic-gradient-based interior-point algorithm for minimizing a continuously differentiable objective function (that may be nonconvex) subject to bound constraints is presented, analyzed, and demonstrated through experimental results. The algorithm is unique from other interior-point methods for solving smooth (nonconvex) optimization problems since the search directions are computed using stochastic gradient estimates. It is also unique in its use of inner neighborhoods of the feasible region -- defined by a positive and vanishing neighborhood-parameter sequence -- in which the iterates are forced to remain. It is shown that with a careful balance between the barrier, step-size, and neighborhood sequences, the proposed algorithm satisfies convergence guarantees in both deterministic and stochastic settings. The results of numerical experiments show that in both settings the algorithm can outperform a projected-(stochastic)-gradient method.

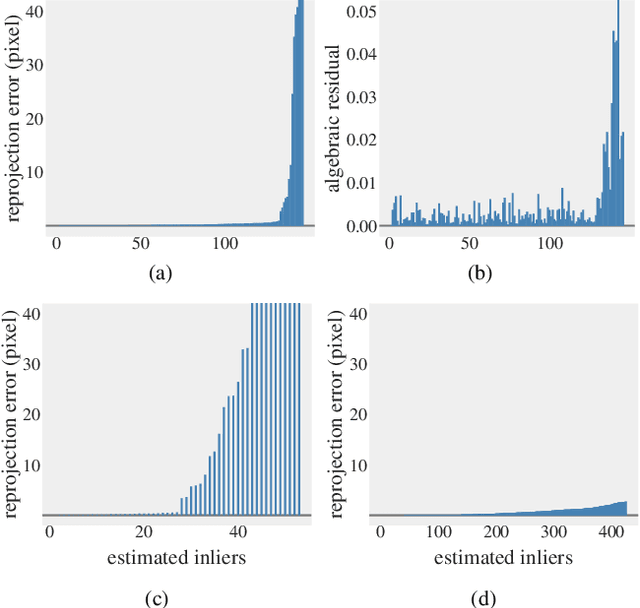
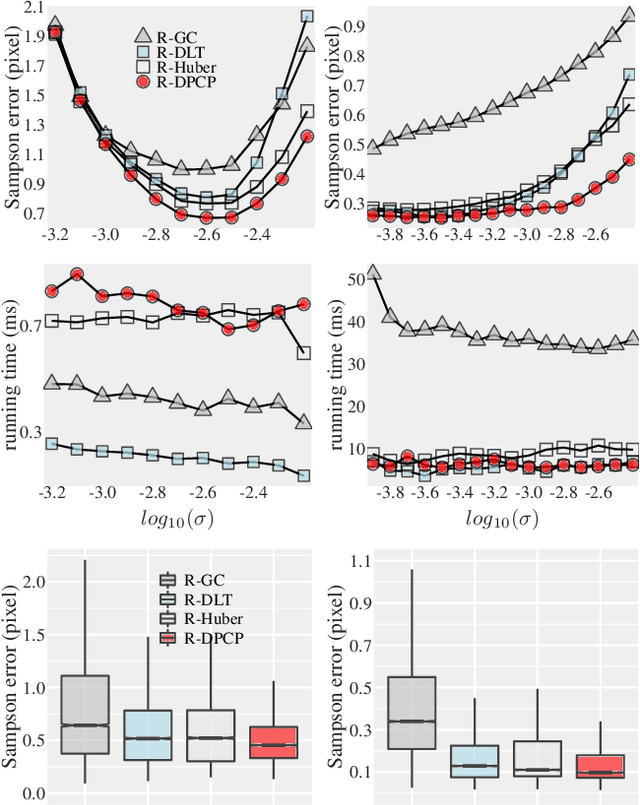
Boosting RANSAC via Dual Principal Component Pursuit

In this paper, we revisit the problem of local optimization in RANSAC. Once a so-far-the-best model has been found, we refine it via Dual Principal Component Pursuit (DPCP), a robust subspace learning method with strong theoretical support and efficient algorithms. The proposed DPCP-RANSAC has far fewer parameters than existing methods and is scalable. Experiments on estimating two-view homographies, fundamental and essential matrices, and three-view homographic tensors using large-scale datasets show that our approach consistently has higher accuracy than state-of-the-art alternatives.

A Stochastic Sequential Quadratic Optimization Algorithm for Nonlinear Equality Constrained Optimization with Rank-Deficient Jacobians

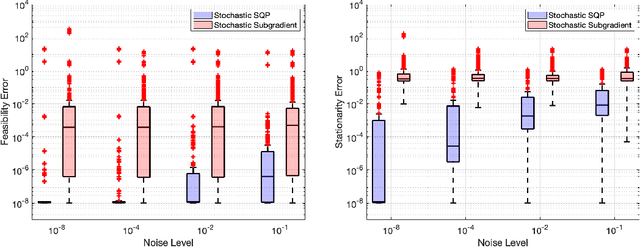
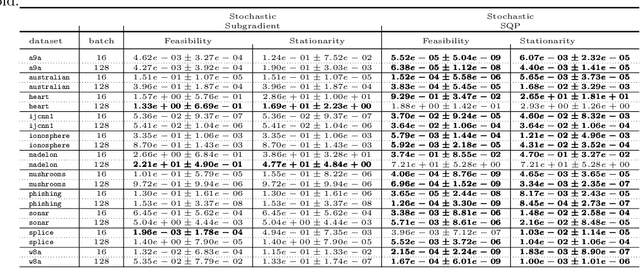
A sequential quadratic optimization algorithm is proposed for solving smooth nonlinear equality constrained optimization problems in which the objective function is defined by an expectation of a stochastic function. The algorithmic structure of the proposed method is based on a step decomposition strategy that is known in the literature to be widely effective in practice, wherein each search direction is computed as the sum of a normal step (toward linearized feasibility) and a tangential step (toward objective decrease in the null space of the constraint Jacobian). However, the proposed method is unique from others in the literature in that it both allows the use of stochastic objective gradient estimates and possesses convergence guarantees even in the setting in which the constraint Jacobians may be rank deficient. The results of numerical experiments demonstrate that the algorithm offers superior performance when compared to popular alternatives.

Sequential Quadratic Optimization for Nonlinear Equality Constrained Stochastic Optimization

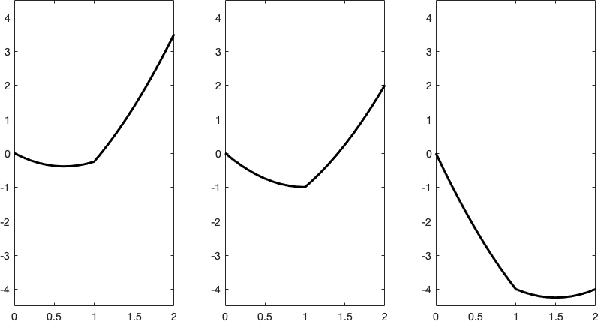
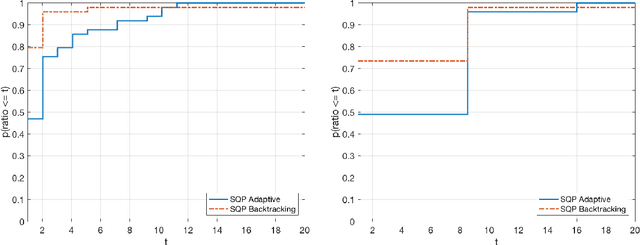
Sequential quadratic optimization algorithms are proposed for solving smooth nonlinear optimization problems with equality constraints. The main focus is an algorithm proposed for the case when the constraint functions are deterministic, and constraint function and derivative values can be computed explicitly, but the objective function is stochastic. It is assumed in this setting that it is intractable to compute objective function and derivative values explicitly, although one can compute stochastic function and gradient estimates. As a starting point for this stochastic setting, an algorithm is proposed for the deterministic setting that is modeled after a state-of-the-art line-search SQP algorithm, but uses a stepsize selection scheme based on Lipschitz constants (or adaptively estimated Lipschitz constants) in place of the line search. This sets the stage for the proposed algorithm for the stochastic setting, for which it is assumed that line searches would be intractable. Under reasonable assumptions, convergence (resp.,~convergence in expectation) from remote starting points is proved for the proposed deterministic (resp.,~stochastic) algorithm. The results of numerical experiments demonstrate the practical performance of our proposed techniques.

Self-Representation Based Unsupervised Exemplar Selection in a Union of Subspaces

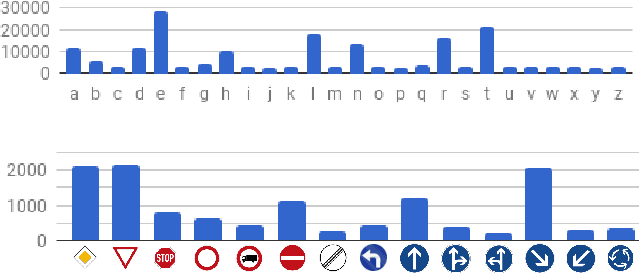
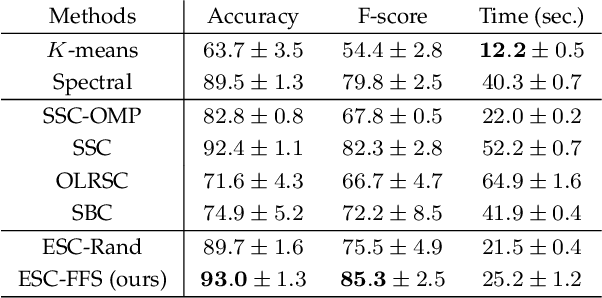
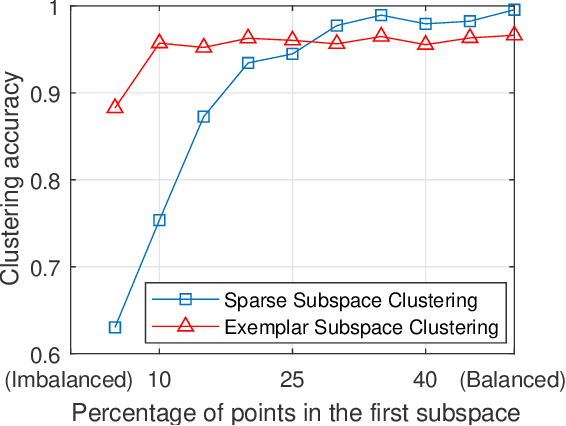
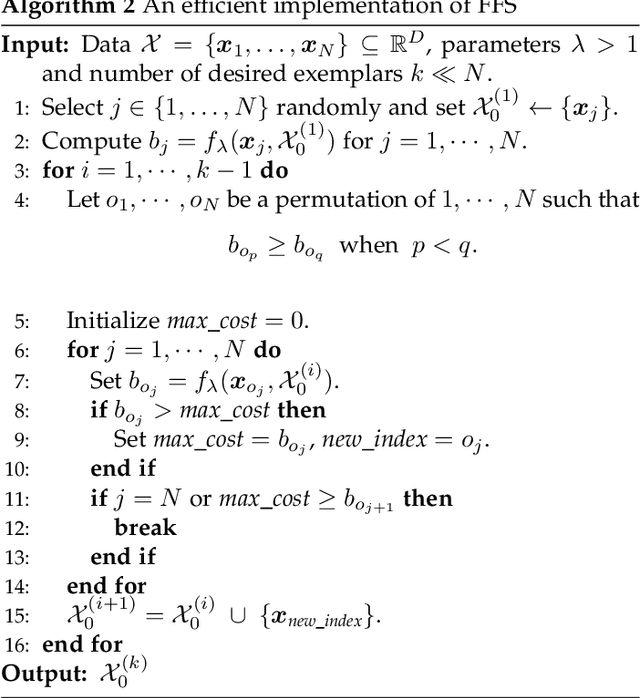
Finding a small set of representatives from an unlabeled dataset is a core problem in a broad range of applications such as dataset summarization and information extraction. Classical exemplar selection methods such as $k$-medoids work under the assumption that the data points are close to a few cluster centroids, and cannot handle the case where data lie close to a union of subspaces. This paper proposes a new exemplar selection model that searches for a subset that best reconstructs all data points as measured by the $\ell_1$ norm of the representation coefficients. Geometrically, this subset best covers all the data points as measured by the Minkowski functional of the subset. To solve our model efficiently, we introduce a farthest first search algorithm that iteratively selects the worst represented point as an exemplar. When the dataset is drawn from a union of independent subspaces, our method is able to select sufficiently many representatives from each subspace. We further develop an exemplar based subspace clustering method that is robust to imbalanced data and efficient for large scale data. Moreover, we show that a classifier trained on the selected exemplars (when they are labeled) can correctly classify the rest of the data points.

Is an Affine Constraint Needed for Affine Subspace Clustering?

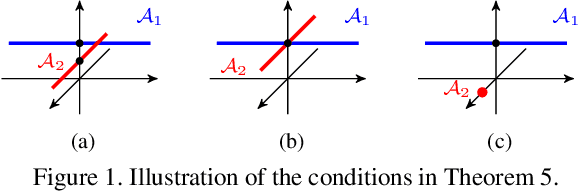
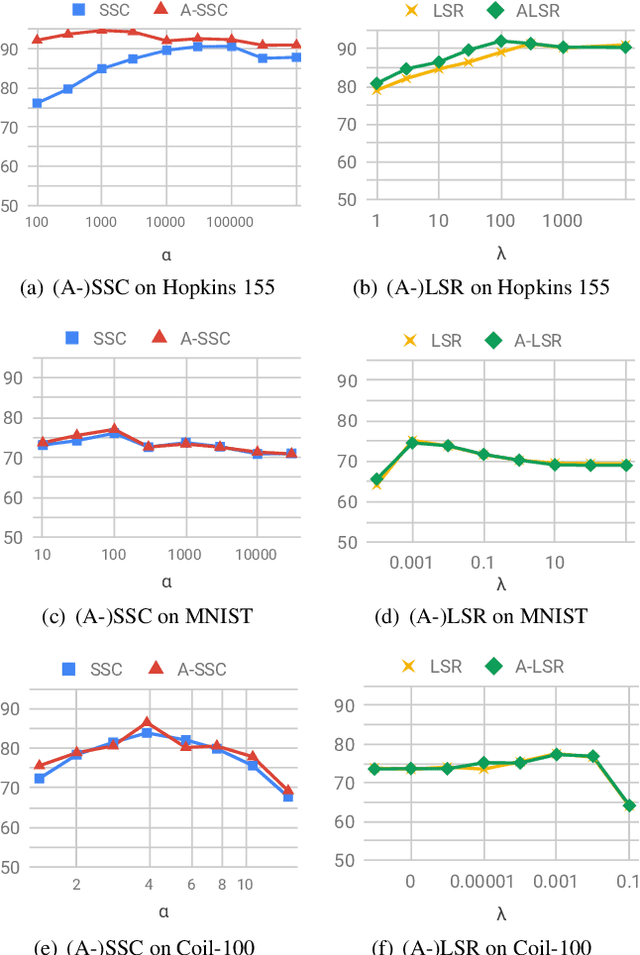
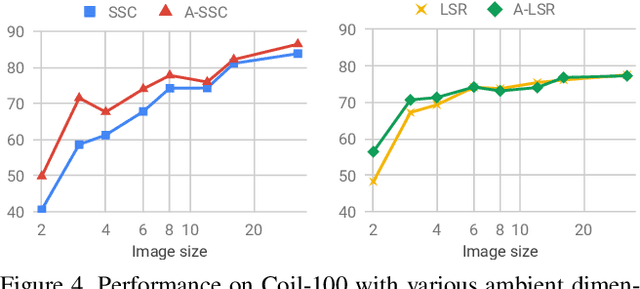
Subspace clustering methods based on expressing each data point as a linear combination of other data points have achieved great success in computer vision applications such as motion segmentation, face and digit clustering. In face clustering, the subspaces are linear and subspace clustering methods can be applied directly. In motion segmentation, the subspaces are affine and an additional affine constraint on the coefficients is often enforced. However, since affine subspaces can always be embedded into linear subspaces of one extra dimension, it is unclear if the affine constraint is really necessary. This paper shows, both theoretically and empirically, that when the dimension of the ambient space is high relative to the sum of the dimensions of the affine subspaces, the affine constraint has a negligible effect on clustering performance. Specifically, our analysis provides conditions that guarantee the correctness of affine subspace clustering methods both with and without the affine constraint, and shows that these conditions are satisfied for high-dimensional data. Underlying our analysis is the notion of affinely independent subspaces, which not only provides geometrically interpretable correctness conditions, but also clarifies the relationships between existing results for affine subspace clustering.

Basis Pursuit and Orthogonal Matching Pursuit for Subspace-preserving Recovery: Theoretical Analysis

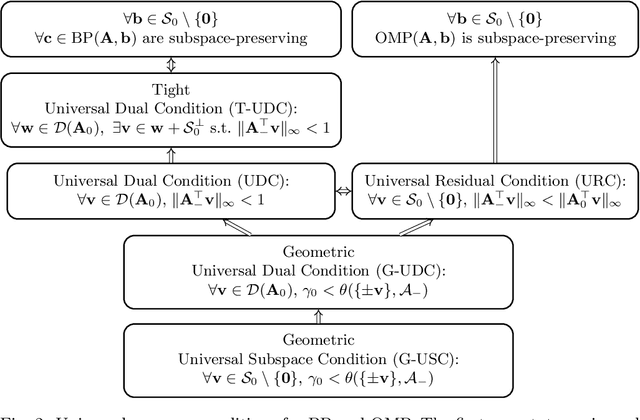
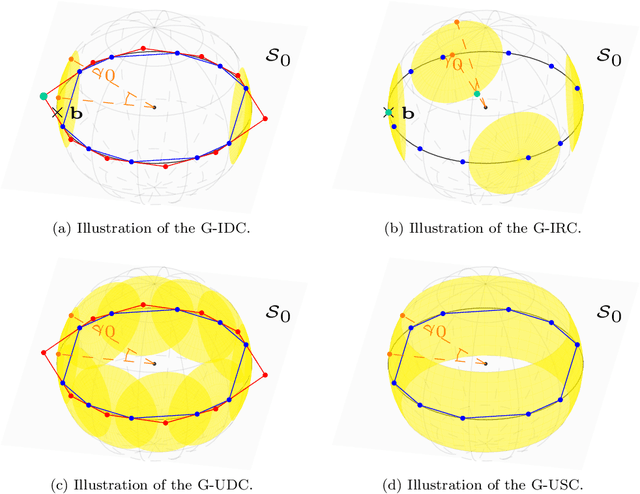
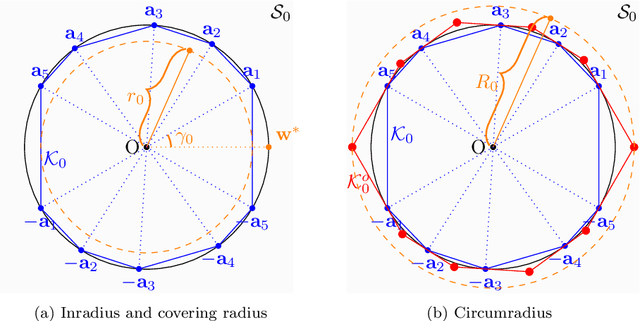
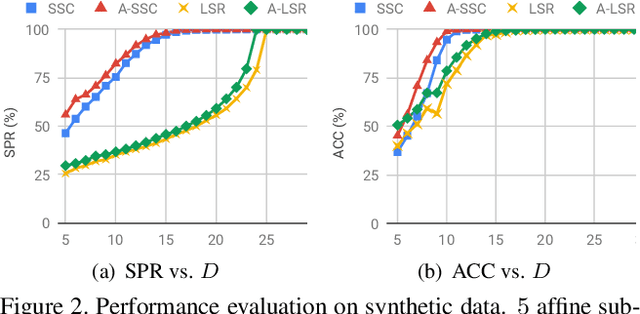
Given an overcomplete dictionary $A$ and a signal $b = Ac^*$ for some sparse vector $c^*$ whose nonzero entries correspond to linearly independent columns of $A$, classical sparse signal recovery theory considers the problem of whether $c^*$ can be recovered as the unique sparsest solution to $b = A c$. It is now well-understood that such recovery is possible by practical algorithms when the dictionary $A$ is incoherent or restricted isometric. In this paper, we consider the more general case where $b$ lies in a subspace $\mathcal{S}_0$ spanned by a subset of linearly dependent columns of $A$, and the remaining columns are outside of the subspace. In this case, the sparsest representation may not be unique, and the dictionary may not be incoherent or restricted isometric. The goal is to have the representation $c$ correctly identify the subspace, i.e. the nonzero entries of $c$ should correspond to columns of $A$ that are in the subspace $\mathcal{S}_0$. Such a representation $c$ is called subspace-preserving, a key concept that has found important applications for learning low-dimensional structures in high-dimensional data. We present various geometric conditions that guarantee subspace-preserving recovery. Among them, the major results are characterized by the covering radius and the angular distance, which capture the distribution of points in the subspace and the similarity between points in the subspace and points outside the subspace, respectively. Importantly, these conditions do not require the dictionary to be incoherent or restricted isometric. By establishing that the subspace-preserving recovery problem and the classical sparse signal recovery problem are equivalent under common assumptions on the latter, we show that several of our proposed conditions are generalizations of some well-known conditions in the sparse signal recovery literature.

Gradient Flows and Accelerated Proximal Splitting Methods

Proximal based algorithms are well-suited to nonsmooth optimization problems with important applications in signal processing, control theory, statistics and machine learning. There are essentially four basic types of proximal algorithms based on fixed-point iteration currently known: forward-backward splitting, forward-backward-forward or Tseng splitting, Douglas-Rachford, and the very recent Davis-Yin three-operator splitting. In addition, the alternating direction method of multipliers (ADMM) is also closely related. In this paper, we show that all these different methods can be derived from the gradient flow by using splitting methods for ordinary differential equations. Furthermore, applying similar discretization scheme to a particular second order differential equation results in accelerated variants of the respective algorithm, which can be of Nesterov or heavy ball type, although we treat both simultaneously. Many of the optimization algorithms we derive are new. For instance, we propose accelerated variants of Davis-Yin and two extensions of ADMM together with their accelerated variants. Interestingly, we show that (accelerated) ADMM corresponds to a rebalanced splitting which is a recent technique designed to preserve steady states of the differential equation. Overall, our results strengthen the connections between optimization and continuous dynamical systems and offer a more unified perspective on accelerated methods.