Online Ad Procurement in Non-stationary Autobidding Worlds

Today's online advertisers procure digital ad impressions through interacting with autobidding platforms: advertisers convey high level procurement goals via setting levers such as budget, target return-on-investment, max cost per click, etc.. Then ads platforms subsequently procure impressions on advertisers' behalf, and report final procurement conversions (e.g. click) to advertisers. In practice, advertisers may receive minimal information on platforms' procurement details, and procurement outcomes are subject to non-stationary factors like seasonal patterns, occasional system corruptions, and market trends which make it difficult for advertisers to optimize lever decisions effectively. Motivated by this, we present an online learning framework that helps advertisers dynamically optimize ad platform lever decisions while subject to general long-term constraints in a realistic bandit feedback environment with non-stationary procurement outcomes. In particular, we introduce a primal-dual algorithm for online decision making with multi-dimension decision variables, bandit feedback and long-term uncertain constraints. We show that our algorithm achieves low regret in many worlds when procurement outcomes are generated through procedures that are stochastic, adversarial, adversarially corrupted, periodic, and ergodic, respectively, without having to know which procedure is the ground truth. Finally, we emphasize that our proposed algorithm and theoretical results extend beyond the applications of online advertising.

A Sequential Quadratic Programming Method with High Probability Complexity Bounds for Nonlinear Equality Constrained Stochastic Optimization

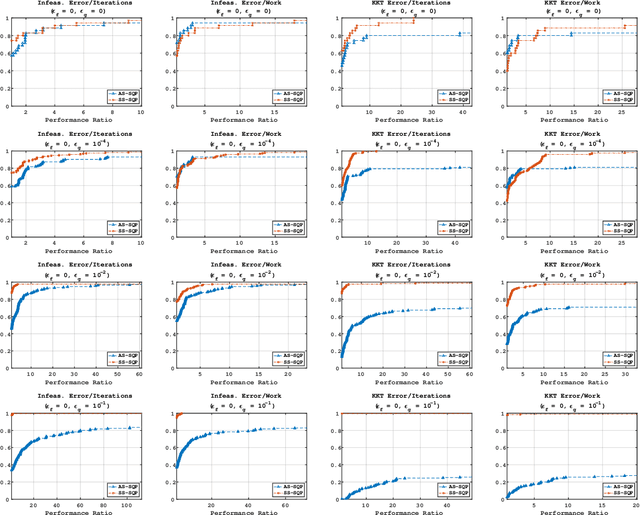
A step-search sequential quadratic programming method is proposed for solving nonlinear equality constrained stochastic optimization problems. It is assumed that constraint function values and derivatives are available, but only stochastic approximations of the objective function and its associated derivatives can be computed via inexact probabilistic zeroth- and first-order oracles. Under reasonable assumptions, a high-probability bound on the iteration complexity of the algorithm to approximate first-order stationarity is derived. Numerical results on standard nonlinear optimization test problems illustrate the advantages and limitations of our proposed method.

Grad-GradaGrad? A Non-Monotone Adaptive Stochastic Gradient Method

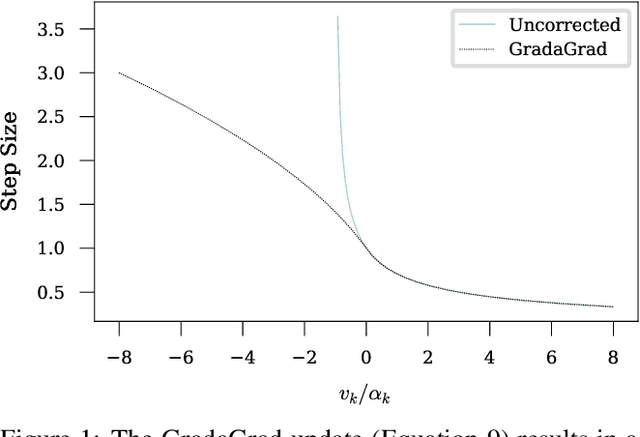
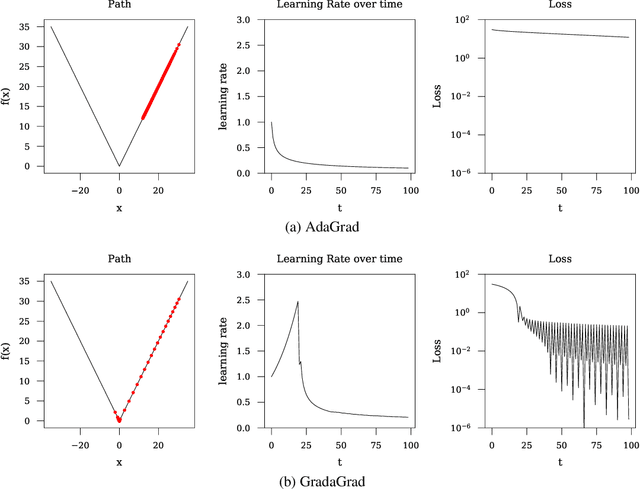
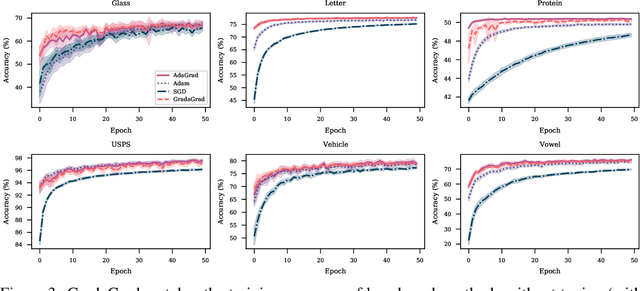
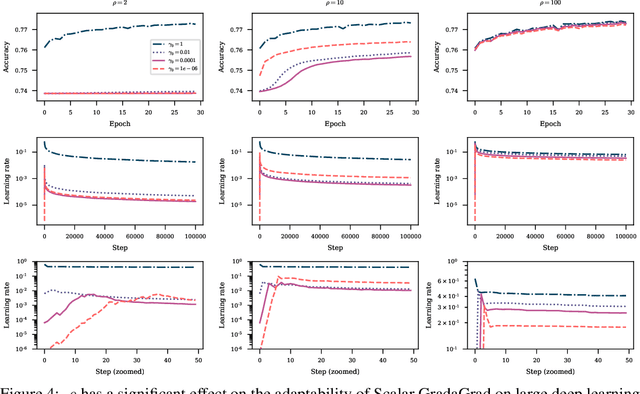
The classical AdaGrad method adapts the learning rate by dividing by the square root of a sum of squared gradients. Because this sum on the denominator is increasing, the method can only decrease step sizes over time, and requires a learning rate scaling hyper-parameter to be carefully tuned. To overcome this restriction, we introduce GradaGrad, a method in the same family that naturally grows or shrinks the learning rate based on a different accumulation in the denominator, one that can both increase and decrease. We show that it obeys a similar convergence rate as AdaGrad and demonstrate its non-monotone adaptation capability with experiments.

Sequential Quadratic Optimization for Nonlinear Equality Constrained Stochastic Optimization

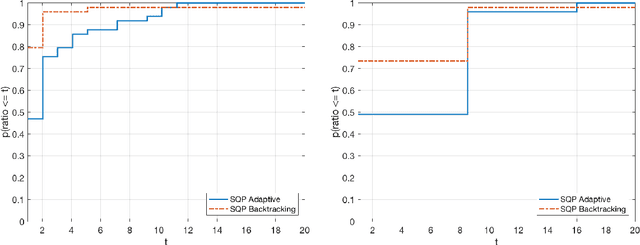
Sequential quadratic optimization algorithms are proposed for solving smooth nonlinear optimization problems with equality constraints. The main focus is an algorithm proposed for the case when the constraint functions are deterministic, and constraint function and derivative values can be computed explicitly, but the objective function is stochastic. It is assumed in this setting that it is intractable to compute objective function and derivative values explicitly, although one can compute stochastic function and gradient estimates. As a starting point for this stochastic setting, an algorithm is proposed for the deterministic setting that is modeled after a state-of-the-art line-search SQP algorithm, but uses a stepsize selection scheme based on Lipschitz constants (or adaptively estimated Lipschitz constants) in place of the line search. This sets the stage for the proposed algorithm for the stochastic setting, for which it is assumed that line searches would be intractable. Under reasonable assumptions, convergence (resp.,~convergence in expectation) from remote starting points is proved for the proposed deterministic (resp.,~stochastic) algorithm. The results of numerical experiments demonstrate the practical performance of our proposed techniques.