Albert Berahas
Sequential Quadratic Optimization for Nonlinear Equality Constrained Stochastic Optimization
Jul 20, 2020
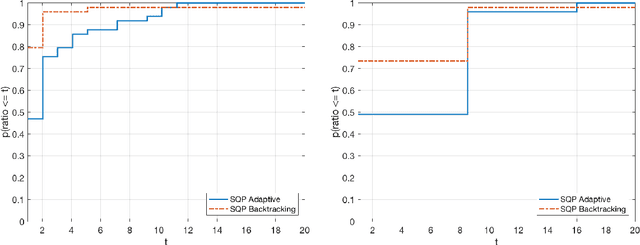

Abstract:Sequential quadratic optimization algorithms are proposed for solving smooth nonlinear optimization problems with equality constraints. The main focus is an algorithm proposed for the case when the constraint functions are deterministic, and constraint function and derivative values can be computed explicitly, but the objective function is stochastic. It is assumed in this setting that it is intractable to compute objective function and derivative values explicitly, although one can compute stochastic function and gradient estimates. As a starting point for this stochastic setting, an algorithm is proposed for the deterministic setting that is modeled after a state-of-the-art line-search SQP algorithm, but uses a stepsize selection scheme based on Lipschitz constants (or adaptively estimated Lipschitz constants) in place of the line search. This sets the stage for the proposed algorithm for the stochastic setting, for which it is assumed that line searches would be intractable. Under reasonable assumptions, convergence (resp.,~convergence in expectation) from remote starting points is proved for the proposed deterministic (resp.,~stochastic) algorithm. The results of numerical experiments demonstrate the practical performance of our proposed techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge