Grad-GradaGrad? A Non-Monotone Adaptive Stochastic Gradient Method
Paper and Code
Jun 14, 2022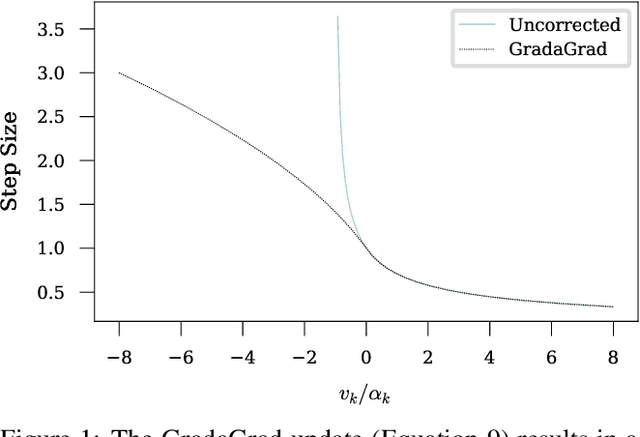
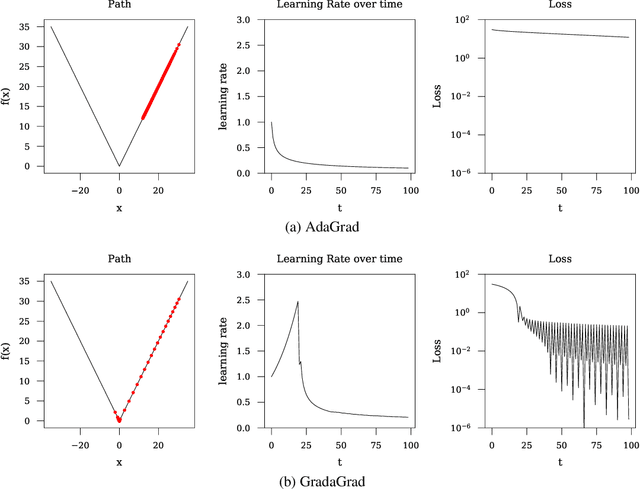
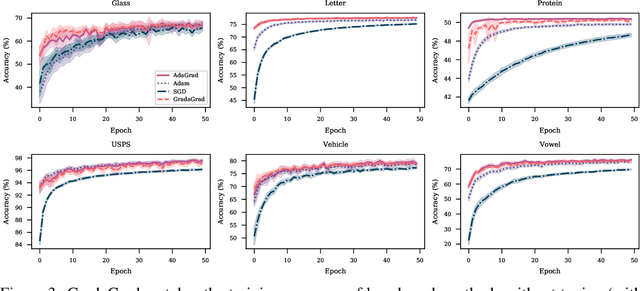
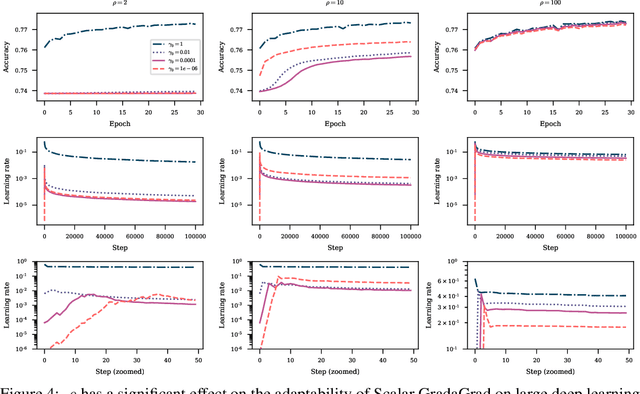
The classical AdaGrad method adapts the learning rate by dividing by the square root of a sum of squared gradients. Because this sum on the denominator is increasing, the method can only decrease step sizes over time, and requires a learning rate scaling hyper-parameter to be carefully tuned. To overcome this restriction, we introduce GradaGrad, a method in the same family that naturally grows or shrinks the learning rate based on a different accumulation in the denominator, one that can both increase and decrease. We show that it obeys a similar convergence rate as AdaGrad and demonstrate its non-monotone adaptation capability with experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge