Basis Pursuit and Orthogonal Matching Pursuit for Subspace-preserving Recovery: Theoretical Analysis
Paper and Code
Dec 30, 2019
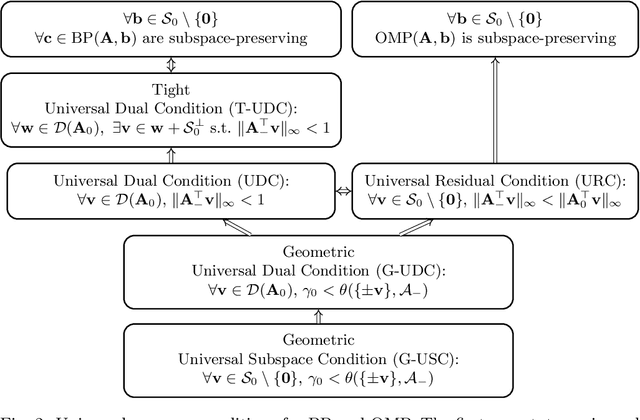
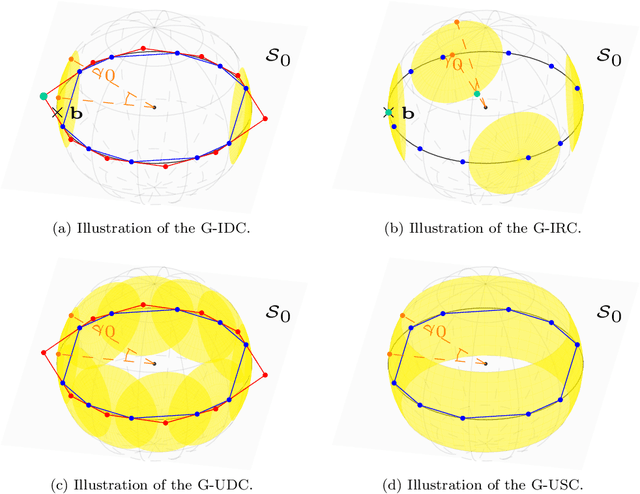
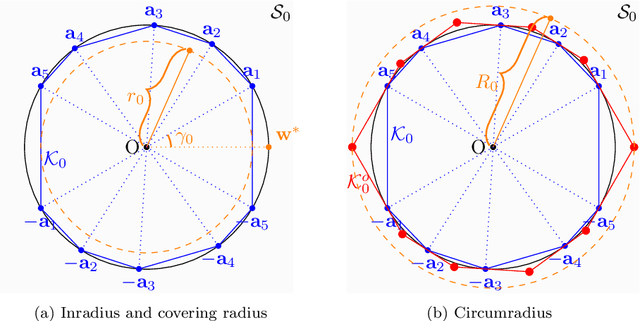
Given an overcomplete dictionary $A$ and a signal $b = Ac^*$ for some sparse vector $c^*$ whose nonzero entries correspond to linearly independent columns of $A$, classical sparse signal recovery theory considers the problem of whether $c^*$ can be recovered as the unique sparsest solution to $b = A c$. It is now well-understood that such recovery is possible by practical algorithms when the dictionary $A$ is incoherent or restricted isometric. In this paper, we consider the more general case where $b$ lies in a subspace $\mathcal{S}_0$ spanned by a subset of linearly dependent columns of $A$, and the remaining columns are outside of the subspace. In this case, the sparsest representation may not be unique, and the dictionary may not be incoherent or restricted isometric. The goal is to have the representation $c$ correctly identify the subspace, i.e. the nonzero entries of $c$ should correspond to columns of $A$ that are in the subspace $\mathcal{S}_0$. Such a representation $c$ is called subspace-preserving, a key concept that has found important applications for learning low-dimensional structures in high-dimensional data. We present various geometric conditions that guarantee subspace-preserving recovery. Among them, the major results are characterized by the covering radius and the angular distance, which capture the distribution of points in the subspace and the similarity between points in the subspace and points outside the subspace, respectively. Importantly, these conditions do not require the dictionary to be incoherent or restricted isometric. By establishing that the subspace-preserving recovery problem and the classical sparse signal recovery problem are equivalent under common assumptions on the latter, we show that several of our proposed conditions are generalizations of some well-known conditions in the sparse signal recovery literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge