Boosting RANSAC via Dual Principal Component Pursuit
Paper and Code
Oct 06, 2021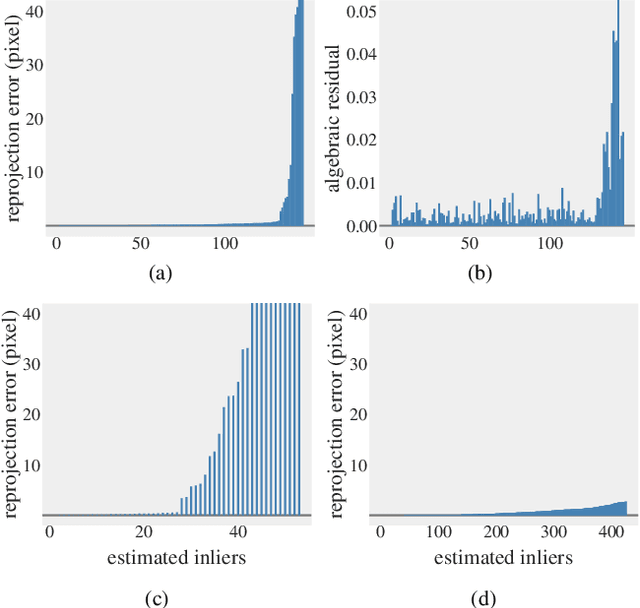


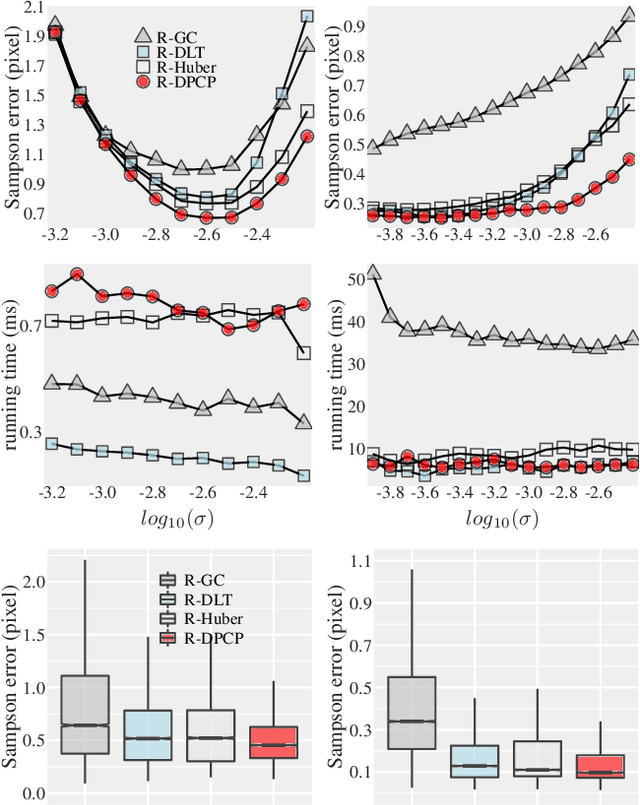
In this paper, we revisit the problem of local optimization in RANSAC. Once a so-far-the-best model has been found, we refine it via Dual Principal Component Pursuit (DPCP), a robust subspace learning method with strong theoretical support and efficient algorithms. The proposed DPCP-RANSAC has far fewer parameters than existing methods and is scalable. Experiments on estimating two-view homographies, fundamental and essential matrices, and three-view homographic tensors using large-scale datasets show that our approach consistently has higher accuracy than state-of-the-art alternatives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge