Cross-Channel Unlabeled Sensing over a Union of Signal Subspaces

Cross-channel unlabeled sensing addresses the problem of recovering a multi-channel signal from measurements that were shuffled across channels. This work expands the cross-channel unlabeled sensing framework to signals that lie in a union of subspaces. The extension allows for handling more complex signal structures and broadens the framework to tasks like compressed sensing. These mismatches between samples and channels often arise in applications such as whole-brain calcium imaging of freely moving organisms or multi-target tracking. We improve over previous models by deriving tighter bounds on the required number of samples for unique reconstruction, while supporting more general signal types. The approach is validated through an application in whole-brain calcium imaging, where organism movements disrupt sample-to-neuron mappings. This demonstrates the utility of our framework in real-world settings with imprecise sample-channel associations, achieving accurate signal reconstruction.

Toeplitz Unlabeled Sensing

Unlabeled sensing is the problem of recovering an element of a vector subspace of R^n, from its image under an unknown permutation of the coordinates and knowledge of the subspace. Here we study this problem for the special class of subspaces that admit a Toeplitz basis.

Online Stability Improvement of Groebner Basis Solvers using Deep Learning

Over the past decade, the Gr\"obner basis theory and automatic solver generation have lead to a large number of solutions to geometric vision problems. In practically all cases, the derived solvers apply a fixed elimination template to calculate the Gr\"obner basis and thereby identify the zero-dimensional variety of the original polynomial constraints. However, it is clear that different variable or monomial orderings lead to different elimination templates, and we show that they may present a large variability in accuracy for a certain instance of a problem. The present paper has two contributions. We first show that for a common class of problems in geometric vision, variable reordering simply translates into a permutation of the columns of the initial coefficient matrix, and that -- as a result -- one and the same elimination template can be reused in different ways, each one leading to potentially different accuracy. We then prove that the original set of coefficients may contain sufficient information to train a classifier for online selection of a good solver, most notably at the cost of only a small computational overhead. We demonstrate wide applicability at the hand of generic dense polynomial problem solvers, as well as a concrete solver from geometric vision.

A Field-Theoretic Approach to Unlabeled Sensing

We study the recent problem of unlabeled sensing from the information sciences in a field-theoretic framework. Our main result asserts that, for sufficiently generic data, the unique solution can be obtained by solving n + 1 polynomial equations in n unknowns.

ARCS: Accurate Rotation and Correspondence Search

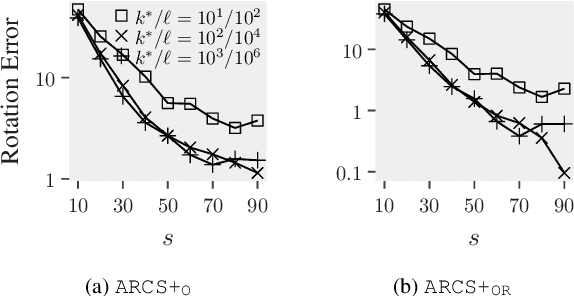
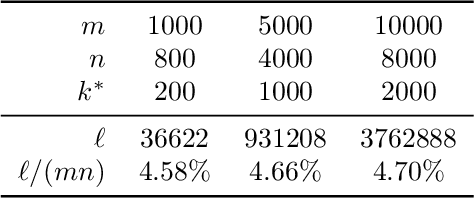
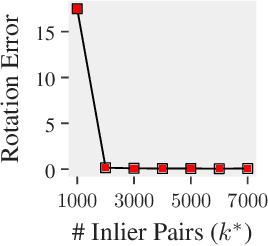
This paper is about the old Wahba problem in its more general form, which we call "simultaneous rotation and correspondence search". In this generalization we need to find a rotation that best aligns two partially overlapping $3$D point sets, of sizes $m$ and $n$ respectively with $m\geq n$. We first propose a solver, $\texttt{ARCS}$, that i) assumes noiseless point sets in general position, ii) requires only $2$ inliers, iii) uses $O(m\log m)$ time and $O(m)$ space, and iv) can successfully solve the problem even with, e.g., $m,n\approx 10^6$ in about $0.1$ seconds. We next robustify $\texttt{ARCS}$ to noise, for which we approximately solve consensus maximization problems using ideas from robust subspace learning and interval stabbing. Thirdly, we refine the approximately found consensus set by a Riemannian subgradient descent approach over the space of unit quaternions, which we show converges globally to an $\varepsilon$-stationary point in $O(\varepsilon^{-4})$ iterations, or locally to the ground-truth at a linear rate in the absence of noise. We combine these algorithms into $\texttt{ARCS+}$, to simultaneously search for rotations and correspondences. Experiments show that $\texttt{ARCS+}$ achieves state-of-the-art performance on large-scale datasets with more than $10^6$ points with a $10^4$ time-speedup over alternative methods. \url{https://github.com/liangzu/ARCS}

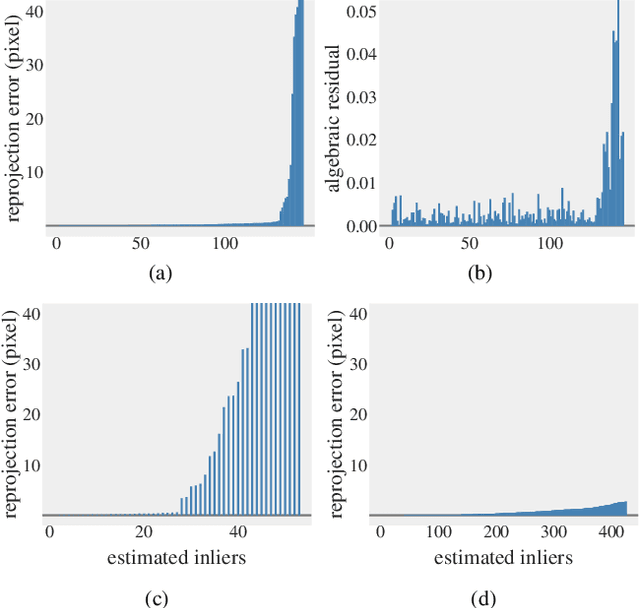
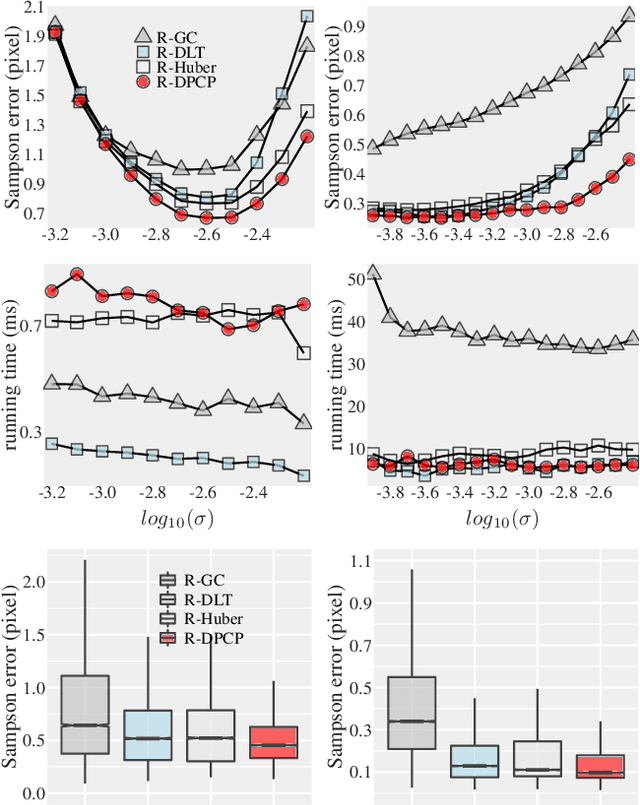
Boosting RANSAC via Dual Principal Component Pursuit

In this paper, we revisit the problem of local optimization in RANSAC. Once a so-far-the-best model has been found, we refine it via Dual Principal Component Pursuit (DPCP), a robust subspace learning method with strong theoretical support and efficient algorithms. The proposed DPCP-RANSAC has far fewer parameters than existing methods and is scalable. Experiments on estimating two-view homographies, fundamental and essential matrices, and three-view homographic tensors using large-scale datasets show that our approach consistently has higher accuracy than state-of-the-art alternatives.

Unlabeled Principal Component Analysis

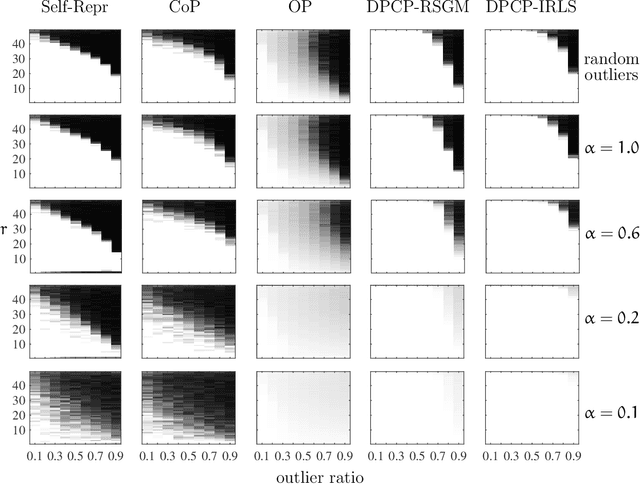
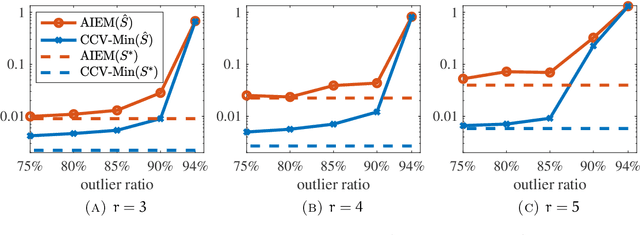
We consider the problem of principal component analysis from a data matrix where the entries of each column have undergone some unknown permutation, termed Unlabeled Principal Component Analysis (UPCA). Using algebraic geometry, we establish that for generic enough data, and up to a permutation of the coordinates of the ambient space, there is a unique subspace of minimal dimension that explains the data. We show that a permutation-invariant system of polynomial equations has finitely many solutions, with each solution corresponding to a row permutation of the ground-truth data matrix. Allowing for missing entries on top of permutations leads to the problem of unlabeled matrix completion, for which we give theoretical results of similar flavor. We also propose a two-stage algorithmic pipeline for UPCA suitable for the practically relevant case where only a fraction of the data has been permuted. Stage-I of this pipeline employs robust-PCA methods to estimate the ground-truth column-space. Equipped with the column-space, stage-II applies methods for linear regression without correspondences to restore the permuted data. A computational study reveals encouraging findings, including the ability of UPCA to handle face images from the Extended Yale-B database with arbitrarily permuted patches of arbitrary size in $0.3$ seconds on a standard desktop computer.

Homomorphic Sensing of Subspace Arrangements

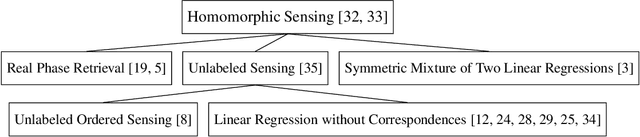
Homomorphic sensing is a recent algebraic-geometric framework that studies the unique recovery of points in a linear subspace from their images under a given collection of linear transformations. It has been successful in interpreting such a recovery in the case of permutations composed by coordinate projections, an important instance in applications known as unlabeled sensing, which models data that are out of order and have missing values. In this paper we make several fundamental contributions. First, we extend the homomorphic sensing framework from a single subspace to a subspace arrangement. Second, when specialized to a single subspace the new conditions are simpler and tighter. Third, as a natural consequence of our main theorem we obtain in a unified way recovery conditions for real phase retrieval, typically known via diverse techniques in the literature, as well as novel conditions for sparse and unsigned versions of linear regression without correspondences and unlabeled sensing. Finally, we prove that the homomorphic sensing property is locally stable to noise.

An exposition to the finiteness of fibers in matrix completion via Plücker coordinates

Matrix completion is a popular paradigm in machine learning and data science, but little is known about the geometric properties of non-random observation patterns. In this paper we study a fundamental geometric analogue of the seminal work of Cand\`es $\&$ Recht, 2009 and Cand\`es $\&$ Tao, 2010, which asks for what kind of observation patterns of size equal to the dimension of the variety of real $m \times n$ rank-$r$ matrices there are finitely many rank-$r$ completions. Our main device is to formulate matrix completion as a hyperplane sections problem on the Grassmannian $\operatorname{Gr}(r,m)$ viewed as a projective variety in Pl\"ucker coordinates.

Linear Regression without Correspondences via Concave Minimization

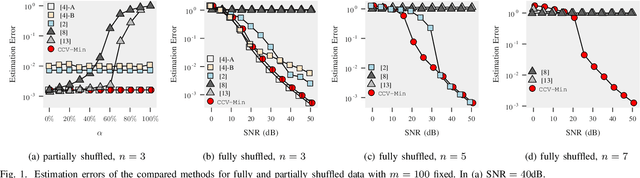
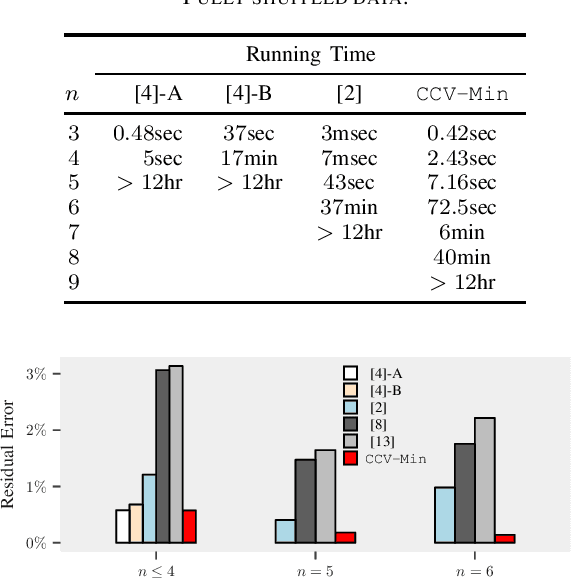
Linear regression without correspondences concerns the recovery of a signal in the linear regression setting, where the correspondences between the observations and the linear functionals are unknown. The associated maximum likelihood function is NP-hard to compute when the signal has dimension larger than one. To optimize this objective function we reformulate it as a concave minimization problem, which we solve via branch-and-bound. This is supported by a computable search space to branch, an effective lower bounding scheme via convex envelope minimization and a refined upper bound, all naturally arising from the concave minimization reformulation. The resulting algorithm outperforms state-of-the-art methods for fully shuffled data and remains tractable for up to $8$-dimensional signals, an untouched regime in prior work.