Homomorphic Sensing of Subspace Arrangements

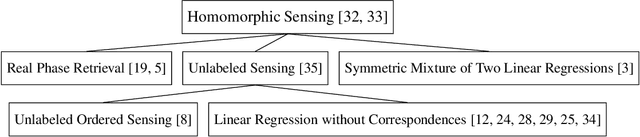
Homomorphic sensing is a recent algebraic-geometric framework that studies the unique recovery of points in a linear subspace from their images under a given collection of linear transformations. It has been successful in interpreting such a recovery in the case of permutations composed by coordinate projections, an important instance in applications known as unlabeled sensing, which models data that are out of order and have missing values. In this paper we make several fundamental contributions. First, we extend the homomorphic sensing framework from a single subspace to a subspace arrangement. Second, when specialized to a single subspace the new conditions are simpler and tighter. Third, as a natural consequence of our main theorem we obtain in a unified way recovery conditions for real phase retrieval, typically known via diverse techniques in the literature, as well as novel conditions for sparse and unsigned versions of linear regression without correspondences and unlabeled sensing. Finally, we prove that the homomorphic sensing property is locally stable to noise.