Unlabeled Principal Component Analysis
Paper and Code
Jan 23, 2021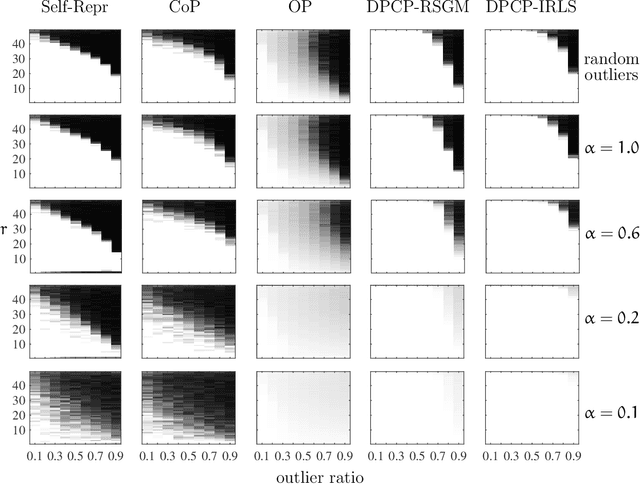
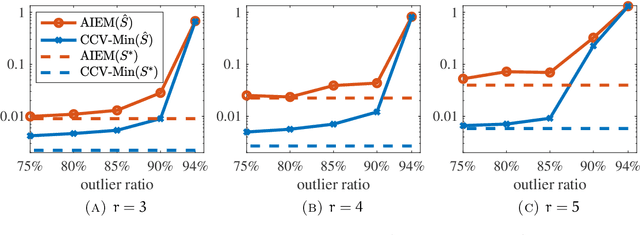


We consider the problem of principal component analysis from a data matrix where the entries of each column have undergone some unknown permutation, termed Unlabeled Principal Component Analysis (UPCA). Using algebraic geometry, we establish that for generic enough data, and up to a permutation of the coordinates of the ambient space, there is a unique subspace of minimal dimension that explains the data. We show that a permutation-invariant system of polynomial equations has finitely many solutions, with each solution corresponding to a row permutation of the ground-truth data matrix. Allowing for missing entries on top of permutations leads to the problem of unlabeled matrix completion, for which we give theoretical results of similar flavor. We also propose a two-stage algorithmic pipeline for UPCA suitable for the practically relevant case where only a fraction of the data has been permuted. Stage-I of this pipeline employs robust-PCA methods to estimate the ground-truth column-space. Equipped with the column-space, stage-II applies methods for linear regression without correspondences to restore the permuted data. A computational study reveals encouraging findings, including the ability of UPCA to handle face images from the Extended Yale-B database with arbitrarily permuted patches of arbitrary size in $0.3$ seconds on a standard desktop computer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge