OAM-Assisted Self-Healing Is Directional, Proportional and Persistent

In this paper we demonstrate the postulated mechanism of self-healing specifically due to orbital-angular-momentum (OAM) in radio vortex beams having equal beam-widths. In previous work we experimentally demonstrated self-healing effects in OAM beams at 28 GHz and postulated a theoretical mechanism to account for them. In this work we further characterize the OAM self-healing mechanism theoretically and confirm those characteristics with systematic and controlled experimental measurements on a 28 GHz outdoor link. Specifically, we find that the OAM self-healing mechanism is an additional self-healing mechanism in structured electromagnetic beams which is directional with respect to the displacement of an obstruction relative to the beam axis. We also confirm our previous findings that the amount of OAM self-healing is proportional to the OAM order, and additionally find that it persists beyond the focusing region into the far field. As such, OAM-assisted self-healing brings an advantage over other so-called non-diffracting beams both in terms of the minimum distance for onset of self-healing and the amount of self-healing obtainable. We relate our findings by extending theoretical models in the literature and develop a unifying electromagnetic analysis to account for self-healing of OAM-bearing non-diffracting beams more rigorously.

Self-Healing Effects in OAM Beams Observed on a 28 GHz Experimental Link

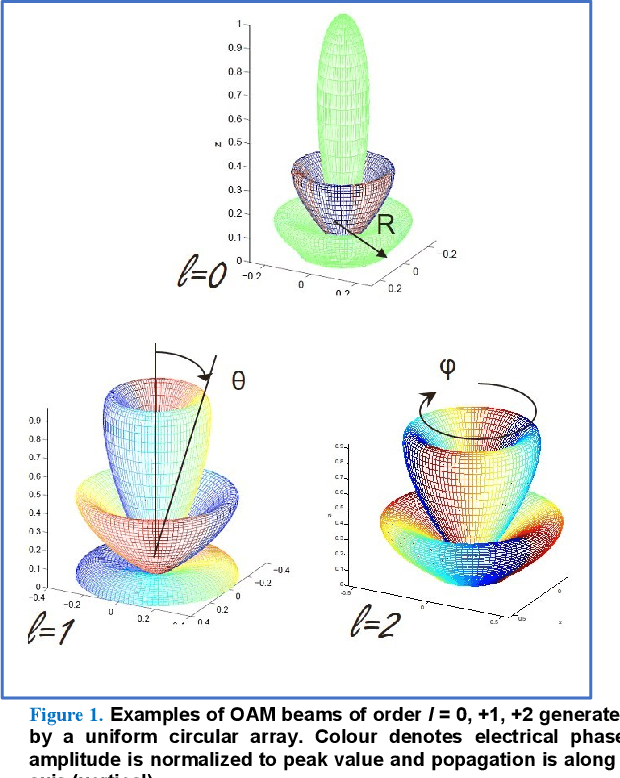
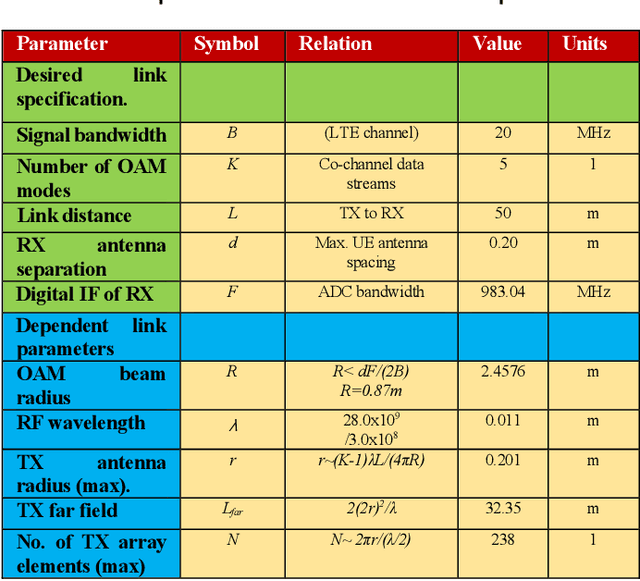
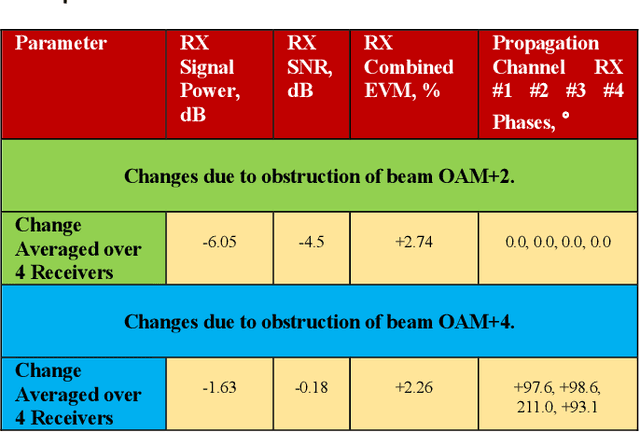
In this paper we document for the first time some of the effects of self-healing, a property of orbital-angular-momentum (OAM) or vortex beams, as observed on a millimeter-wave experimental communications link in an outdoors line-of-sight (LOS) scenario. The OAM beams have a helical phase and polarization structure and have conical amplitude shape in the far field. The Poynting vectors of the OAM beams also possess helical structures, orthogonal to the corresponding helical phase-fronts. Due to such non-planar structure in the direction orthogonal to the beam axis, OAM beams are a subset of structured light beams. Such structured beams are known to possess self-healing properties when partially obstructed along their propagation axis, especially in their near fields, resulting in partial reconstruction of their structures at larger distances along their beam axis. Various theoretical rationales have been proposed to explain, model and experimentally verify the self-healing physical effects in structured optical beams, using various types of obstructions and experimental techniques. Based on these models, we hypothesize that any self-healing observed will be greater as the OAM order increases. Here we observe the self-healing effects for the first time in structured OAM radio beams, in terms of communication signals and channel parameters rather than beam structures. We capture the effects of partial near-field obstructions of OAM beams of different orders on the communications signals and provide a physical rationale to substantiate that the self-healing effect was observed to increase with the order of OAM, agreeing with our hypothesis.

Online Stability Improvement of Groebner Basis Solvers using Deep Learning

Over the past decade, the Gr\"obner basis theory and automatic solver generation have lead to a large number of solutions to geometric vision problems. In practically all cases, the derived solvers apply a fixed elimination template to calculate the Gr\"obner basis and thereby identify the zero-dimensional variety of the original polynomial constraints. However, it is clear that different variable or monomial orderings lead to different elimination templates, and we show that they may present a large variability in accuracy for a certain instance of a problem. The present paper has two contributions. We first show that for a common class of problems in geometric vision, variable reordering simply translates into a permutation of the columns of the initial coefficient matrix, and that -- as a result -- one and the same elimination template can be reused in different ways, each one leading to potentially different accuracy. We then prove that the original set of coefficients may contain sufficient information to train a classifier for online selection of a good solver, most notably at the cost of only a small computational overhead. We demonstrate wide applicability at the hand of generic dense polynomial problem solvers, as well as a concrete solver from geometric vision.

Incremental Semantic Localization using Hierarchical Clustering of Object Association Sets

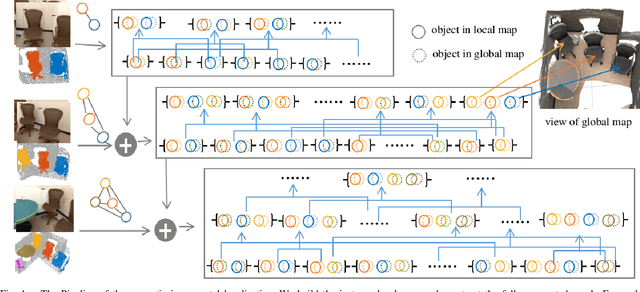
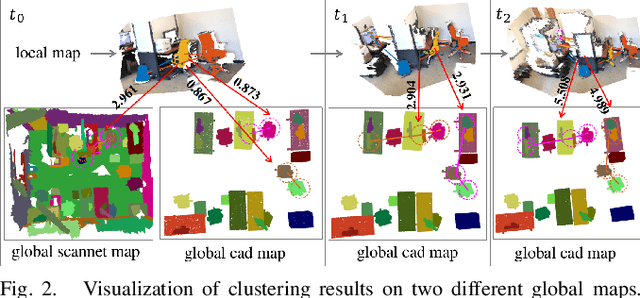
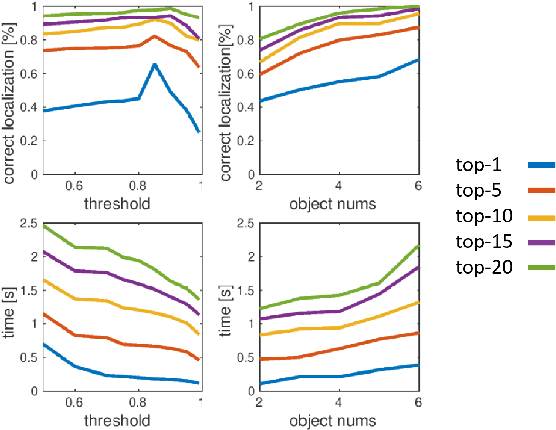
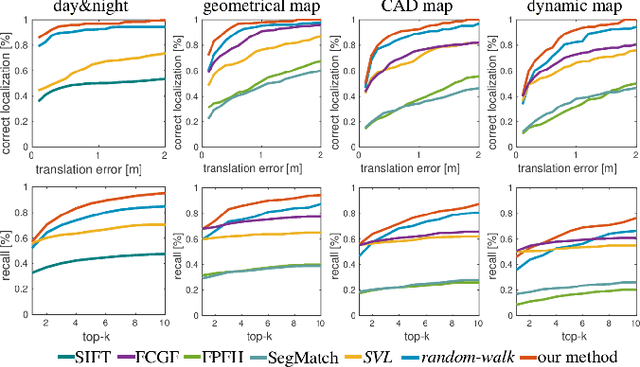
We present a novel approach for relocalization or place recognition, a fundamental problem to be solved in many robotics, automation, and AR applications. Rather than relying on often unstable appearance information, we consider a situation in which the reference map is given in the form of localized objects. Our localization framework relies on 3D semantic object detections, which are then associated to objects in the map. Possible pair-wise association sets are grown based on hierarchical clustering using a merge metric that evaluates spatial compatibility. The latter notably uses information about relative object configurations, which is invariant with respect to global transformations. Association sets are furthermore updated and expanded as the camera incrementally explores the environment and detects further objects. We test our algorithm in several challenging situations including dynamic scenes, large view-point changes, and scenes with repeated instances. Our experiments demonstrate that our approach outperforms prior art in terms of both robustness and accuracy.

Accurate Instance-Level CAD Model Retrieval in a Large-Scale Database

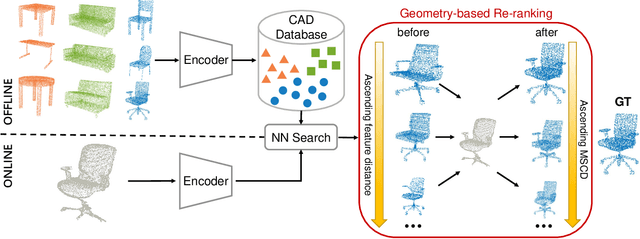
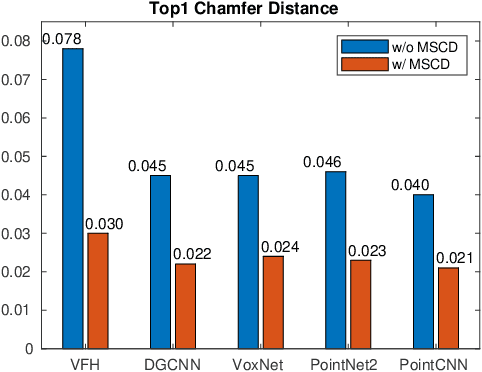
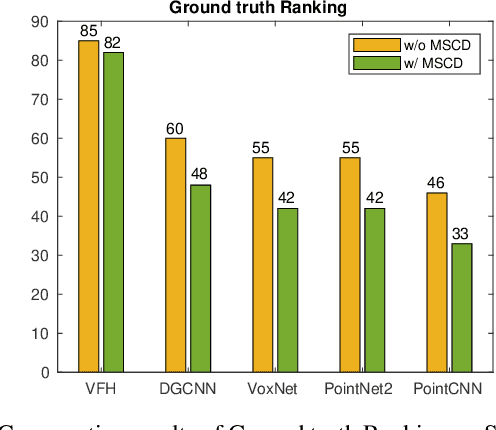
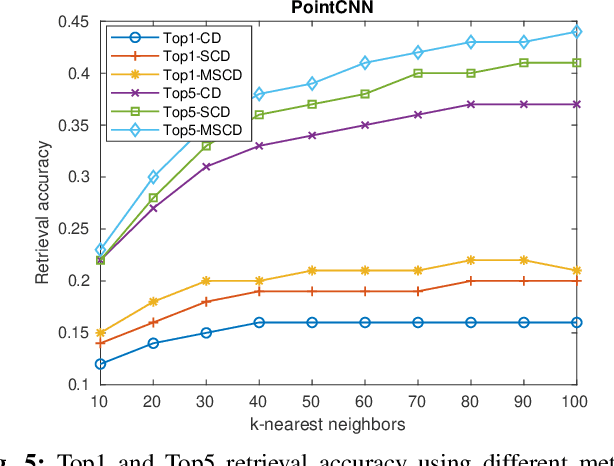
We present a new solution to the fine-grained retrieval of clean CAD models from a large-scale database in order to recover detailed object shape geometries for RGBD scans. Unlike previous work simply indexing into a moderately small database using an object shape descriptor and accepting the top retrieval result, we argue that in the case of a large-scale database a more accurate model may be found within a neighborhood of the descriptor. More importantly, we propose that the distinctiveness deficiency of shape descriptors at the instance level can be compensated by a geometry-based re-ranking of its neighborhood. Our approach first leverages the discriminative power of learned representations to distinguish between different categories of models and then uses a novel robust point set distance metric to re-rank the CAD neighborhood, enabling fine-grained retrieval in a large shape database. Evaluation on a real-world dataset shows that our geometry-based re-ranking is a conceptually simple but highly effective method that can lead to a significant improvement in retrieval accuracy compared to the state-of-the-art.

Globally optimal point set registration by joint symmetry plane fitting

The present work proposes a solution to the challenging problem of registering two partial point sets of the same object with very limited overlap. We leverage the fact that most objects found in man-made environments contain a plane of symmetry. By reflecting the points of each set with respect to the plane of symmetry, we can largely increase the overlap between the sets and therefore boost the registration process. However, prior knowledge about the plane of symmetry is generally unavailable or at least very hard to find, especially with limited partial views, and finding this plane could strongly benefit from a prior alignment of the partial point sets. We solve this chicken-and-egg problem by jointly optimizing the relative pose and symmetry plane parameters, and notably do so under global optimality by employing the branch-and-bound (BnB) paradigm. Our results demonstrate a great improvement over the current state-of-the-art in globally optimal point set registration for common objects. We furthermore show an interesting application of our method to dense 3D reconstruction of scenes with repetitive objects.

Deep-SLAM++: Object-level RGBD SLAM based on class-specific deep shape priors

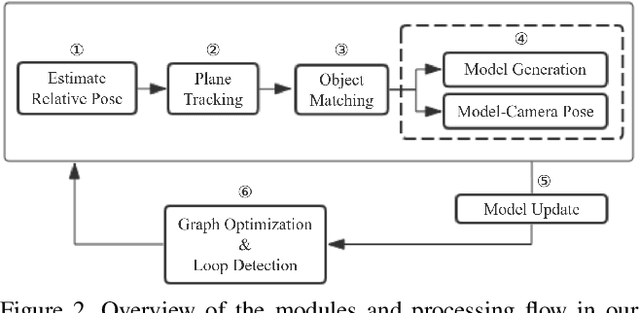
In an effort to increase the capabilities of SLAM systems and produce object-level representations, the community increasingly investigates the imposition of higher-level priors into the estimation process. One such example is given by employing object detectors to load and register full CAD models. Our work extends this idea to environments with unknown objects and imposes object priors by employing modern class-specific neural networks to generate complete model geometry proposals. The difficulty of using such predictions in a real SLAM scenario is that the prediction performance depends on the view-point and measurement quality, with even small changes of the input data sometimes leading to a large variability in the network output. We propose a discrete selection strategy that finds the best among multiple proposals from different registered views by re-enforcing the agreement with the online depth measurements. The result is an effective object-level RGBD SLAM system that produces compact, high-fidelity, and dense 3D maps with semantic annotations. It outperforms traditional fusion strategies in terms of map completeness and resilience against degrading measurement quality.

Dense Object Reconstruction from RGBD Images with Embedded Deep Shape Representations

Most problems involving simultaneous localization and mapping can nowadays be solved using one of two fundamentally different approaches. The traditional approach is given by a least-squares objective, which minimizes many local photometric or geometric residuals over explicitly parametrized structure and camera parameters. Unmodeled effects violating the lambertian surface assumption or geometric invariances of individual residuals are encountered through statistical averaging or the addition of robust kernels and smoothness terms. Aiming at more accurate measurement models and the inclusion of higher-order shape priors, the community more recently shifted its attention to deep end-to-end models for solving geometric localization and mapping problems. However, at test-time, these feed-forward models ignore the more traditional geometric or photometric consistency terms, thus leading to a low ability to recover fine details and potentially complete failure in corner case scenarios. With an application to dense object modeling from RGBD images, our work aims at taking the best of both worlds by embedding modern higher-order object shape priors into classical iterative residual minimization objectives. We demonstrate a general ability to improve mapping accuracy with respect to each modality alone, and present a successful application to real data.