ARCS: Accurate Rotation and Correspondence Search
Paper and Code
Mar 29, 2022
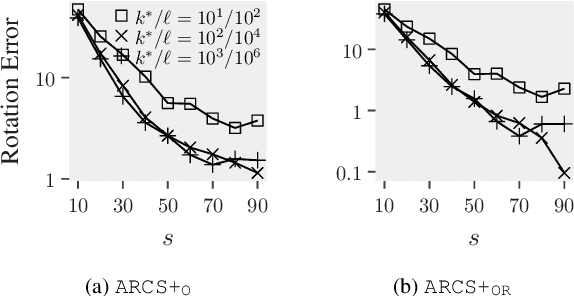
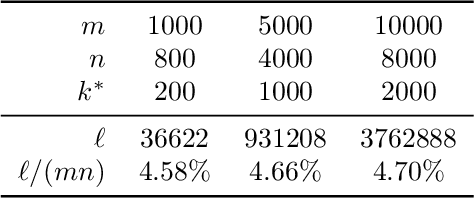
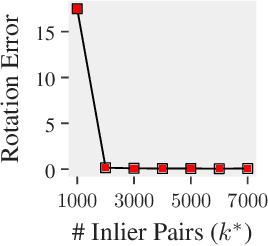
This paper is about the old Wahba problem in its more general form, which we call "simultaneous rotation and correspondence search". In this generalization we need to find a rotation that best aligns two partially overlapping $3$D point sets, of sizes $m$ and $n$ respectively with $m\geq n$. We first propose a solver, $\texttt{ARCS}$, that i) assumes noiseless point sets in general position, ii) requires only $2$ inliers, iii) uses $O(m\log m)$ time and $O(m)$ space, and iv) can successfully solve the problem even with, e.g., $m,n\approx 10^6$ in about $0.1$ seconds. We next robustify $\texttt{ARCS}$ to noise, for which we approximately solve consensus maximization problems using ideas from robust subspace learning and interval stabbing. Thirdly, we refine the approximately found consensus set by a Riemannian subgradient descent approach over the space of unit quaternions, which we show converges globally to an $\varepsilon$-stationary point in $O(\varepsilon^{-4})$ iterations, or locally to the ground-truth at a linear rate in the absence of noise. We combine these algorithms into $\texttt{ARCS+}$, to simultaneously search for rotations and correspondences. Experiments show that $\texttt{ARCS+}$ achieves state-of-the-art performance on large-scale datasets with more than $10^6$ points with a $10^4$ time-speedup over alternative methods. \url{https://github.com/liangzu/ARCS}
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge