Linear Regression without Correspondences via Concave Minimization
Paper and Code
Mar 17, 2020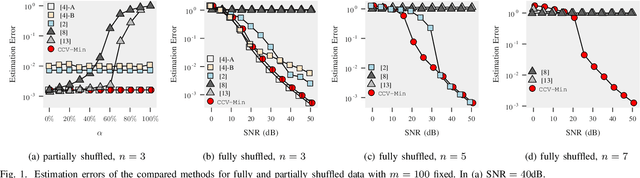
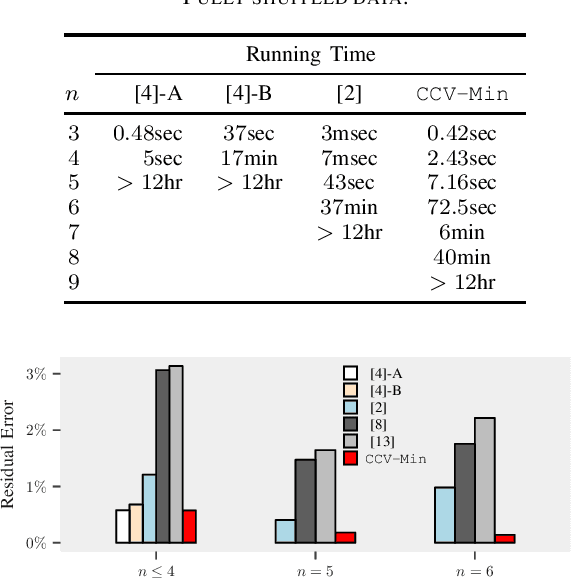
Linear regression without correspondences concerns the recovery of a signal in the linear regression setting, where the correspondences between the observations and the linear functionals are unknown. The associated maximum likelihood function is NP-hard to compute when the signal has dimension larger than one. To optimize this objective function we reformulate it as a concave minimization problem, which we solve via branch-and-bound. This is supported by a computable search space to branch, an effective lower bounding scheme via convex envelope minimization and a refined upper bound, all naturally arising from the concave minimization reformulation. The resulting algorithm outperforms state-of-the-art methods for fully shuffled data and remains tractable for up to $8$-dimensional signals, an untouched regime in prior work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge