DNT: a Deeply Normalized Transformer that can be trained by Momentum SGD

Transformers have become the de facto backbone of modern deep learning, yet their training typically demands an advanced optimizer with adaptive learning rate like AdamW, rather than a momentum SGDW (mSGDW). Previous works show that it is mainly due to a heavy-tailed distribution of the gradients. In this paper, we introduce a Deeply Normalized Transformer (DNT), which is meticulously engineered to overcome this limitation enabling seamless training with vanilla mSGDW while yielding comparable performance to the Transformers trained via AdamW. To be specific, in DNT, we strategically integrate normalization techniques at proper positions in the Transformers to effectively modulate the Jacobian matrices of each layer, balance the influence of weights, activations, and their interactions, and thus enable the distributions of gradients concentrated. We provide both theoretical justifications of the normalization technique used in our DNT and extensive empirical evaluation on two popular Transformer architectures to validate that: a) DNT outperforms its counterparts (\ie, ViT and GPT), and b) DNT can be effectively trained with vanilla mSGDW.

Taming Transformer Without Using Learning Rate Warmup

Scaling Transformer to a large scale without using some technical tricks such as learning rate warump and using an obviously lower learning rate is an extremely challenging task, and is increasingly gaining more attention. In this paper, we provide a theoretical analysis for the process of training Transformer and reveal the rationale behind the model crash phenomenon in the training process, termed \textit{spectral energy concentration} of ${\bW_q}^{\top} \bW_k$, which is the reason for a malignant entropy collapse, where ${\bW_q}$ and $\bW_k$ are the projection matrices for the query and the key in Transformer, respectively. To remedy this problem, motivated by \textit{Weyl's Inequality}, we present a novel optimization strategy, \ie, making the weight updating in successive steps smooth -- if the ratio $\frac{\sigma_{1}(\nabla \bW_t)}{\sigma_{1}(\bW_{t-1})}$ is larger than a threshold, we will automatically bound the learning rate to a weighted multiple of $\frac{\sigma_{1}(\bW_{t-1})}{\sigma_{1}(\nabla \bW_t)}$, where $\nabla \bW_t$ is the updating quantity in step $t$. Such an optimization strategy can prevent spectral energy concentration to only a few directions, and thus can avoid malignant entropy collapse which will trigger the model crash. We conduct extensive experiments using ViT, Swin-Transformer and GPT, showing that our optimization strategy can effectively and stably train these Transformers without using learning rate warmup.

Exploring a Principled Framework for Deep Subspace Clustering

Subspace clustering is a classical unsupervised learning task, built on a basic assumption that high-dimensional data can be approximated by a union of subspaces (UoS). Nevertheless, the real-world data are often deviating from the UoS assumption. To address this challenge, state-of-the-art deep subspace clustering algorithms attempt to jointly learn UoS representations and self-expressive coefficients. However, the general framework of the existing algorithms suffers from a catastrophic feature collapse and lacks a theoretical guarantee to learn desired UoS representation. In this paper, we present a Principled fRamewOrk for Deep Subspace Clustering (PRO-DSC), which is designed to learn structured representations and self-expressive coefficients in a unified manner. Specifically, in PRO-DSC, we incorporate an effective regularization on the learned representations into the self-expressive model, prove that the regularized self-expressive model is able to prevent feature space collapse, and demonstrate that the learned optimal representations under certain condition lie on a union of orthogonal subspaces. Moreover, we provide a scalable and efficient approach to implement our PRO-DSC and conduct extensive experiments to verify our theoretical findings and demonstrate the superior performance of our proposed deep subspace clustering approach. The code is available at https://github.com/mengxianghan123/PRO-DSC.

Neural Normalized Cut: A Differential and Generalizable Approach for Spectral Clustering

Spectral clustering, as a popular tool for data clustering, requires an eigen-decomposition step on a given affinity to obtain the spectral embedding. Nevertheless, such a step suffers from the lack of generalizability and scalability. Moreover, the obtained spectral embeddings can hardly provide a good approximation to the ground-truth partition and thus a k-means step is adopted to quantize the embedding. In this paper, we propose a simple yet effective scalable and generalizable approach, called Neural Normalized Cut (NeuNcut), to learn the clustering membership for spectral clustering directly. In NeuNcut, we properly reparameterize the unknown cluster membership via a neural network, and train the neural network via stochastic gradient descent with a properly relaxed normalized cut loss. As a result, our NeuNcut enjoys a desired generalization ability to directly infer clustering membership for out-of-sample unseen data and hence brings us an efficient way to handle clustering task with ultra large-scale data. We conduct extensive experiments on both synthetic data and benchmark datasets and experimental results validate the effectiveness and the superiority of our approach. Our code is available at: https://github.com/hewei98/NeuNcut.

Rethinking Decoders for Transformer-based Semantic Segmentation: Compression is All You Need

State-of-the-art methods for Transformer-based semantic segmentation typically adopt Transformer decoders that are used to extract additional embeddings from image embeddings via cross-attention, refine either or both types of embeddings via self-attention, and project image embeddings onto the additional embeddings via dot-product. Despite their remarkable success, these empirical designs still lack theoretical justifications or interpretations, thus hindering potentially principled improvements. In this paper, we argue that there are fundamental connections between semantic segmentation and compression, especially between the Transformer decoders and Principal Component Analysis (PCA). From such a perspective, we derive a white-box, fully attentional DEcoder for PrIncipled semantiC segemenTation (DEPICT), with the interpretations as follows: 1) the self-attention operator refines image embeddings to construct an ideal principal subspace that aligns with the supervision and retains most information; 2) the cross-attention operator seeks to find a low-rank approximation of the refined image embeddings, which is expected to be a set of orthonormal bases of the principal subspace and corresponds to the predefined classes; 3) the dot-product operation yields compact representation for image embeddings as segmentation masks. Experiments conducted on dataset ADE20K find that DEPICT consistently outperforms its black-box counterpart, Segmenter, and it is light weight and more robust.

MaskCL: Semantic Mask-Driven Contrastive Learning for Unsupervised Person Re-Identification with Clothes Change

This paper considers a novel and challenging problem: unsupervised long-term person re-identification with clothes change. Unfortunately, conventional unsupervised person re-id methods are designed for short-term cases and thus fail to perceive clothes-independent patterns due to simply being driven by RGB prompt. To tackle with such a bottleneck, we propose a semantic mask-driven contrastive learning approach, in which silhouette masks are embedded into contrastive learning framework as the semantic prompts and cross-clothes invariance is learnt from hierarchically semantic neighbor structure by combining both RGB and semantic features in a two-branches network. Since such a challenging re-id task setting is investigated for the first time, we conducted extensive experiments to evaluate state-of-the-art unsupervised short-term person re-id methods on five widely-used clothes-change re-id datasets. Experimental results verify that our approach outperforms the unsupervised re-id competitors by a clear margin, remaining a narrow gap to the supervised baselines.

Hybrid Contrastive Learning with Cluster Ensemble for Unsupervised Person Re-identification

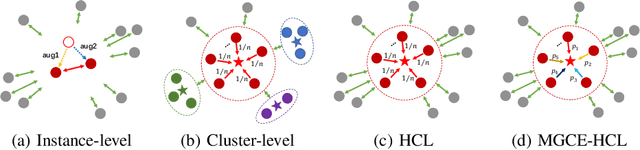
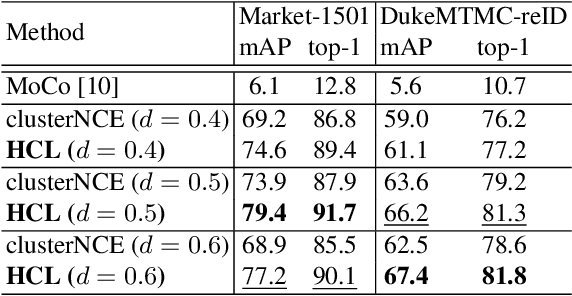
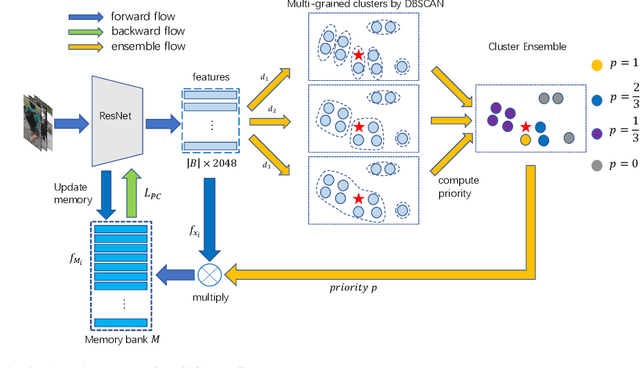
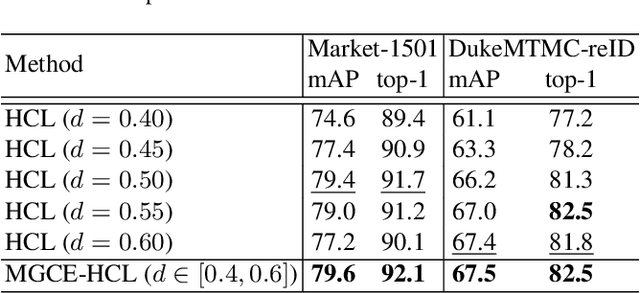
Unsupervised person re-identification (ReID) aims to match a query image of a pedestrian to the images in gallery set without supervision labels. The most popular approaches to tackle unsupervised person ReID are usually performing a clustering algorithm to yield pseudo labels at first and then exploit the pseudo labels to train a deep neural network. However, the pseudo labels are noisy and sensitive to the hyper-parameter(s) in clustering algorithm. In this paper, we propose a Hybrid Contrastive Learning (HCL) approach for unsupervised person ReID, which is based on a hybrid between instance-level and cluster-level contrastive loss functions. Moreover, we present a Multi-Granularity Clustering Ensemble based Hybrid Contrastive Learning (MGCE-HCL) approach, which adopts a multi-granularity clustering ensemble strategy to mine priority information among the pseudo positive sample pairs and defines a priority-weighted hybrid contrastive loss for better tolerating the noises in the pseudo positive samples. We conduct extensive experiments on two benchmark datasets Market-1501 and DukeMTMC-reID. Experimental results validate the effectiveness of our proposals.

Learning a Self-Expressive Network for Subspace Clustering

State-of-the-art subspace clustering methods are based on self-expressive model, which represents each data point as a linear combination of other data points. However, such methods are designed for a finite sample dataset and lack the ability to generalize to out-of-sample data. Moreover, since the number of self-expressive coefficients grows quadratically with the number of data points, their ability to handle large-scale datasets is often limited. In this paper, we propose a novel framework for subspace clustering, termed Self-Expressive Network (SENet), which employs a properly designed neural network to learn a self-expressive representation of the data. We show that our SENet can not only learn the self-expressive coefficients with desired properties on the training data, but also handle out-of-sample data. Besides, we show that SENet can also be leveraged to perform subspace clustering on large-scale datasets. Extensive experiments conducted on synthetic data and real world benchmark data validate the effectiveness of the proposed method. In particular, SENet yields highly competitive performance on MNIST, Fashion MNIST and Extended MNIST and state-of-the-art performance on CIFAR-10. The code is available at https://github.com/zhangsz1998/Self-Expressive-Network.

Cluster-guided Asymmetric Contrastive Learning for Unsupervised Person Re-Identification

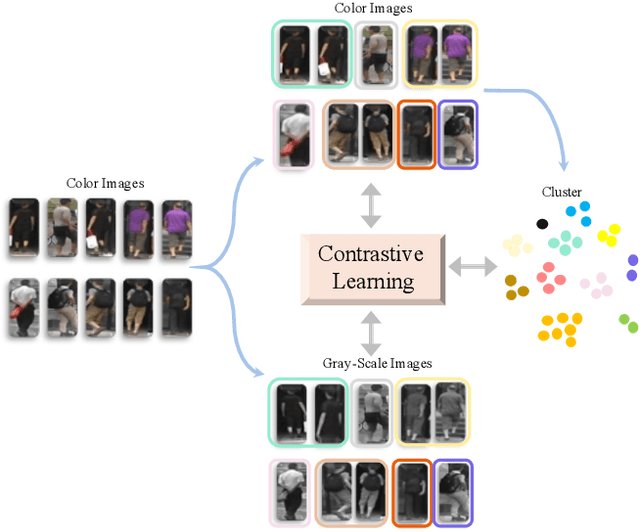
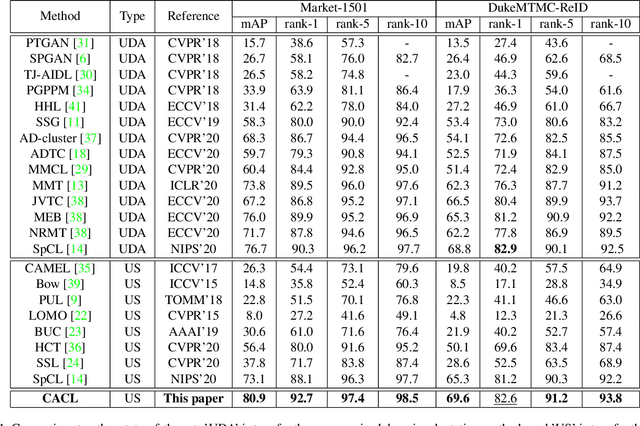
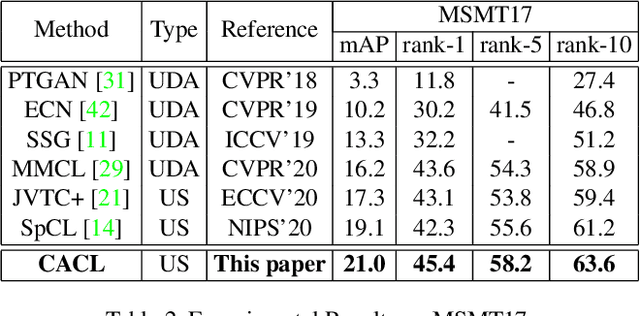
Unsupervised person re-identification (Re-ID) aims to match pedestrian images from different camera views in unsupervised setting. Existing methods for unsupervised person Re-ID are usually built upon the pseudo labels from clustering. However, the quality of clustering depends heavily on the quality of the learned features, which are overwhelmingly dominated by the colors in images especially in the unsupervised setting. In this paper, we propose a Cluster-guided Asymmetric Contrastive Learning (CACL) approach for unsupervised person Re-ID, in which cluster structure is leveraged to guide the feature learning in a properly designed asymmetric contrastive learning framework. To be specific, we propose a novel cluster-level contrastive loss to help the siamese network effectively mine the invariance in feature learning with respect to the cluster structure within and between different data augmentation views, respectively. Extensive experiments conducted on three benchmark datasets demonstrate superior performance of our proposal.

Learning Graph Normalization for Graph Neural Networks

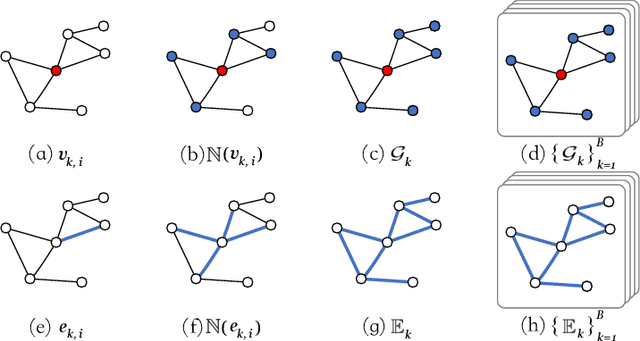
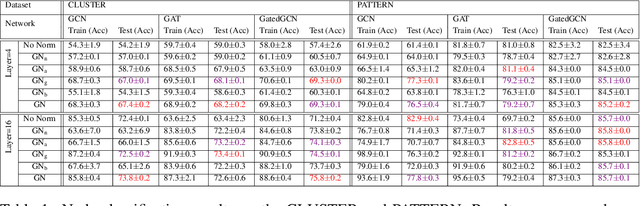
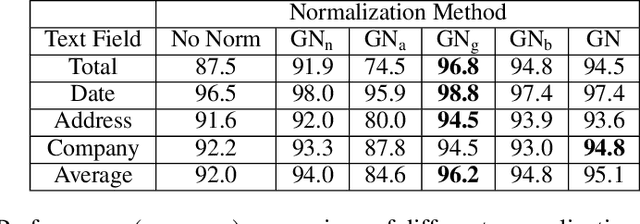
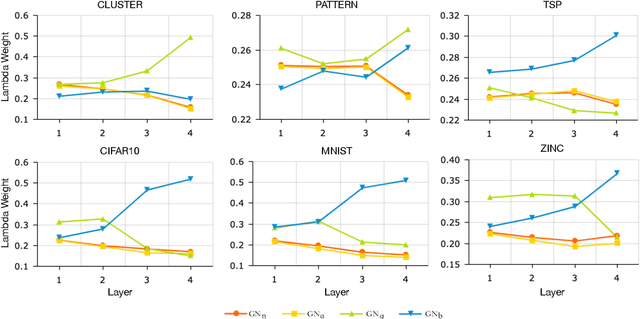
Graph Neural Networks (GNNs) have attracted considerable attention and have emerged as a new promising paradigm to process graph-structured data. GNNs are usually stacked to multiple layers and the node representations in each layer are computed through propagating and aggregating the neighboring node features with respect to the graph. By stacking to multiple layers, GNNs are able to capture the long-range dependencies among the data on the graph and thus bring performance improvements. To train a GNN with multiple layers effectively, some normalization techniques (e.g., node-wise normalization, batch-wise normalization) are necessary. However, the normalization techniques for GNNs are highly task-relevant and different application tasks prefer to different normalization techniques, which is hard to know in advance. To tackle this deficiency, in this paper, we propose to learn graph normalization by optimizing a weighted combination of normalization techniques at four different levels, including node-wise normalization, adjacency-wise normalization, graph-wise normalization, and batch-wise normalization, in which the adjacency-wise normalization and the graph-wise normalization are newly proposed in this paper to take into account the local structure and the global structure on the graph, respectively. By learning the optimal weights, we are able to automatically select a single best or a best combination of multiple normalizations for a specific task. We conduct extensive experiments on benchmark datasets for different tasks, including node classification, link prediction, graph classification and graph regression, and confirm that the learned graph normalization leads to competitive results and that the learned weights suggest the appropriate normalization techniques for the specific task. Source code is released here https://github.com/cyh1112/GraphNormalization.