Optimal Activation Functions for the Random Features Regression Model

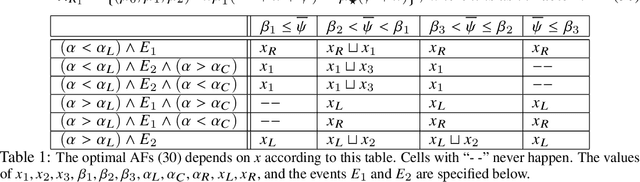
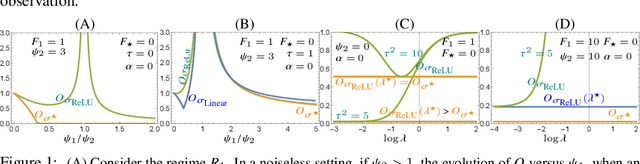
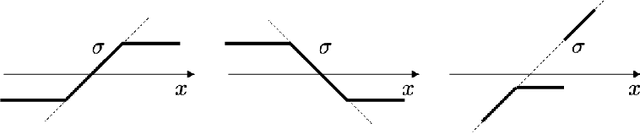
The asymptotic mean squared test error and sensitivity of the Random Features Regression model (RFR) have been recently studied. We build on this work and identify in closed-form the family of Activation Functions (AFs) that minimize a combination of the test error and sensitivity of the RFR under different notions of functional parsimony. We find scenarios under which the optimal AFs are linear, saturated linear functions, or expressible in terms of Hermite polynomials. Finally, we show how using optimal AFs impacts well-established properties of the RFR model, such as its double descent curve, and the dependency of its optimal regularization parameter on the observation noise level.

Distributed Optimization, Averaging via ADMM, and Network Topology

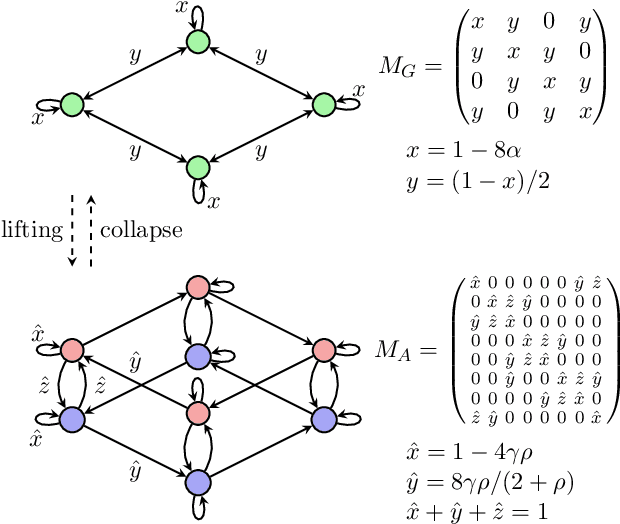
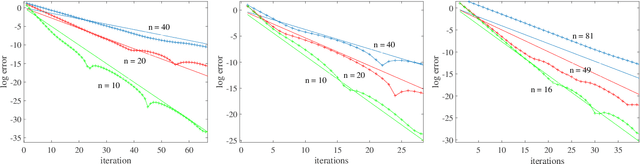
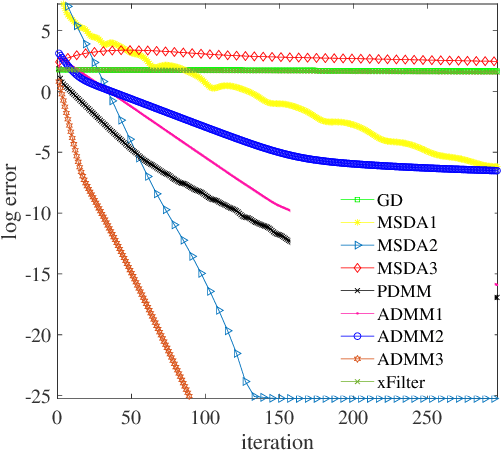
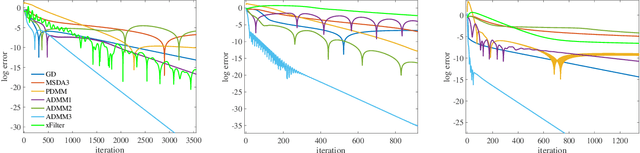
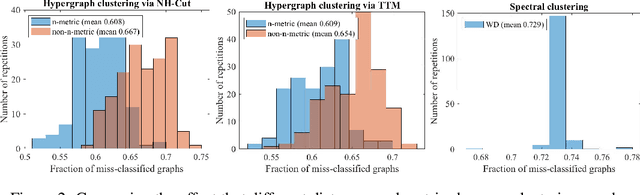
There has been an increasing necessity for scalable optimization methods, especially due to the explosion in the size of datasets and model complexity in modern machine learning applications. Scalable solvers often distribute the computation over a network of processing units. For simple algorithms such as gradient descent the dependency of the convergence time with the topology of this network is well-known. However, for more involved algorithms such as the Alternating Direction Methods of Multipliers (ADMM) much less is known. At the heart of many distributed optimization algorithms there exists a gossip subroutine which averages local information over the network, and whose efficiency is crucial for the overall performance of the method. In this paper we review recent research in this area and, with the goal of isolating such a communication exchange behaviour, we compare different algorithms when applied to a canonical distributed averaging consensus problem. We also show interesting connections between ADMM and lifted Markov chains besides providing an explicitly characterization of its convergence and optimal parameter tuning in terms of spectral properties of the network. Finally, we empirically study the connection between network topology and convergence rates for different algorithms on a real world problem of sensor localization.

Multi-Marginal Optimal Transport Defines a Generalized Metric

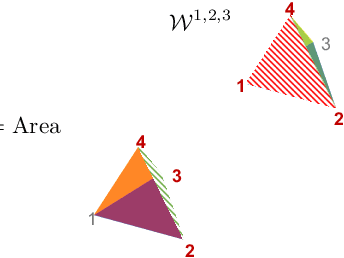
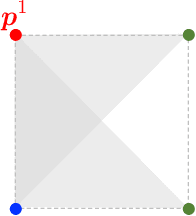
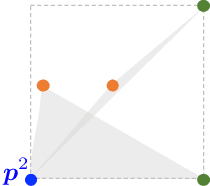
We prove that the multi-marginal optimal transport (MMOT) problem defines a generalized metric. In addition, we prove that the distance induced by MMOT satisfies a generalized triangle inequality that, to leading order, cannot be improved.

Exact inference under the perfect phylogeny model

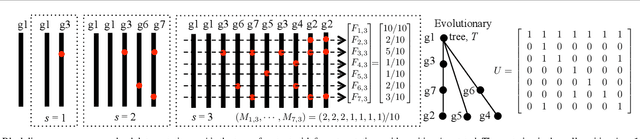
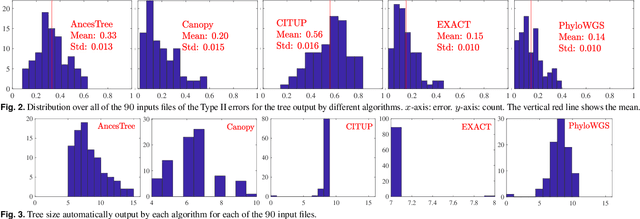
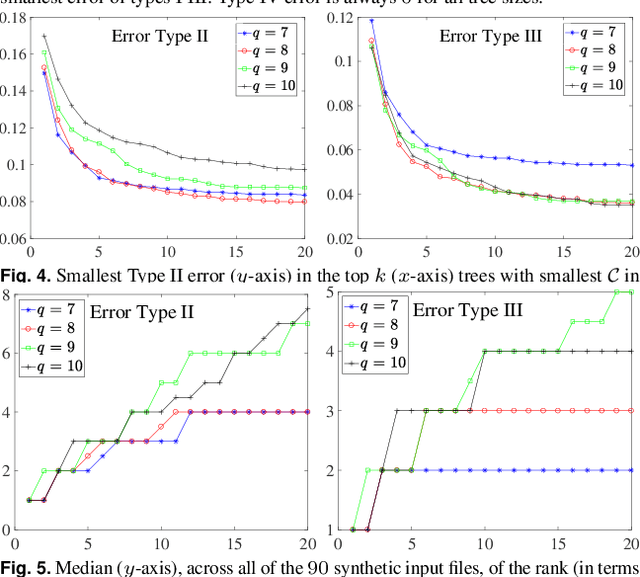
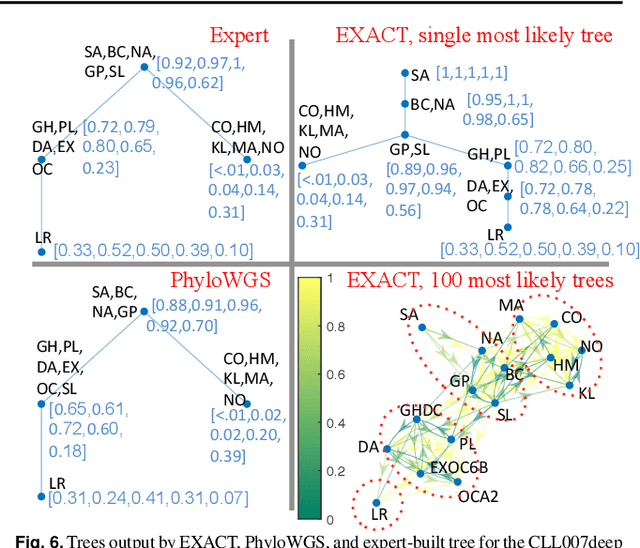
Motivation: Many inference tools use the Perfect Phylogeny Model (PPM) to learn trees from noisy variant allele frequency (VAF) data. Learning in this setting is hard, and existing tools use approximate or heuristic algorithms. An algorithmic improvement is important to help disentangle the limitations of the PPM's assumptions from the limitations in our capacity to learn under it. Results: We make such improvement in the scenario, where the mutations that are relevant for evolution can be clustered into a small number of groups, and the trees to be reconstructed have a small number of nodes. We use a careful combination of algorithms, software, and hardware, to develop EXACT: a tool that can explore the space of all possible phylogenetic trees, and performs exact inference under the PPM with noisy data. EXACT allows users to obtain not just the most-likely tree for some input data, but exact statistics about the distribution of trees that might explain the data. We show that EXACT outperforms several existing tools for this same task. Availability: https://github.com/surjray-repos/EXACT

Genome-scale estimation of cellular objectives

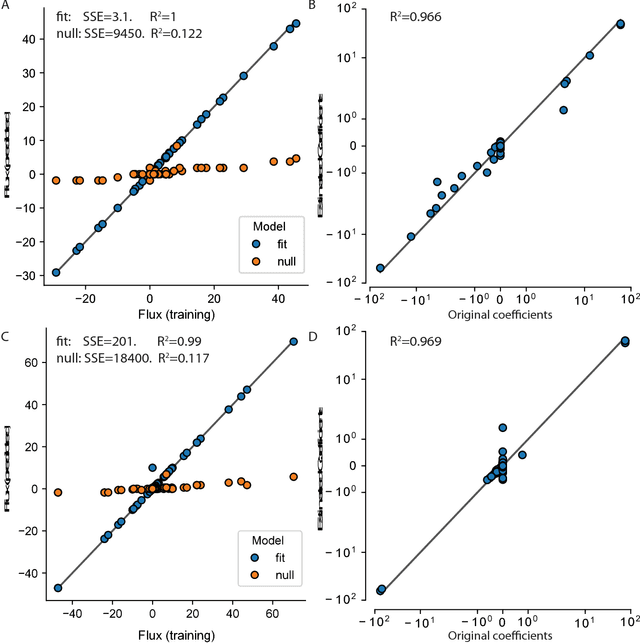
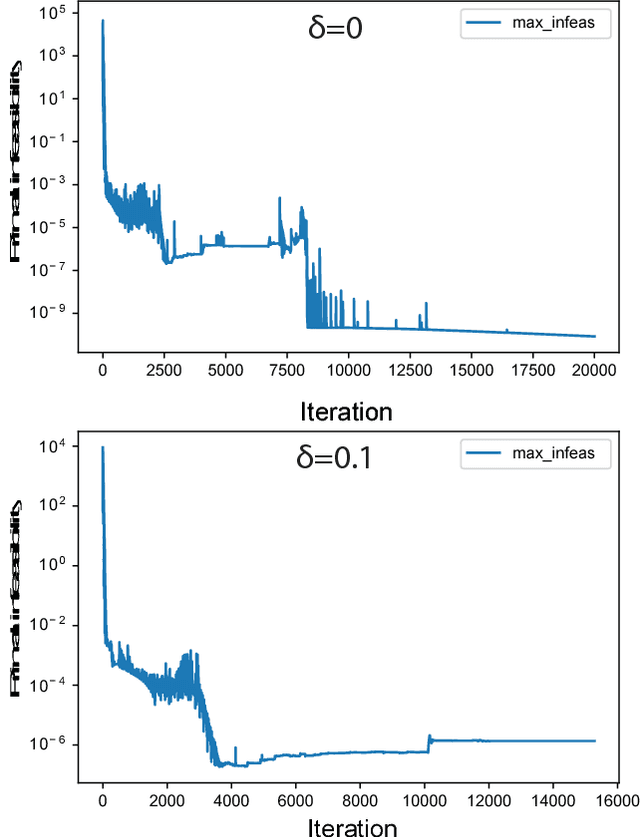
Cellular metabolism is predicted accurately at the genome-scale using constraint based modeling. Such predictions typically rely on optimizing an assumed cellular objective function, which takes the form of a stoichiometrically-determined reaction such as biomass synthesis, ATP yield, or reactive oxygen species formation. While these objective functions are typically constructed by hand, several algorithms have been developed to estimate them from data. Generally, two approaches for data-driven objective estimation exist: estimating objective weights for existing reactions, and de novo generation of a new objective reaction. The latter approach can discover objectives that are not describable as a linear combination of existing reactions. However, it requires solving a nonconvex optimization problem and its scalability to genome-scale models has not been demonstrated. Here, we develop a new algorithm that extends existing approaches for de novo objective generation and solve it using the alternating direction method of multipliers (ADMM). We demonstrate our approach on a genome-scale model and show that it identifies de novo objectives from measured fluxes with tunable sparsity.

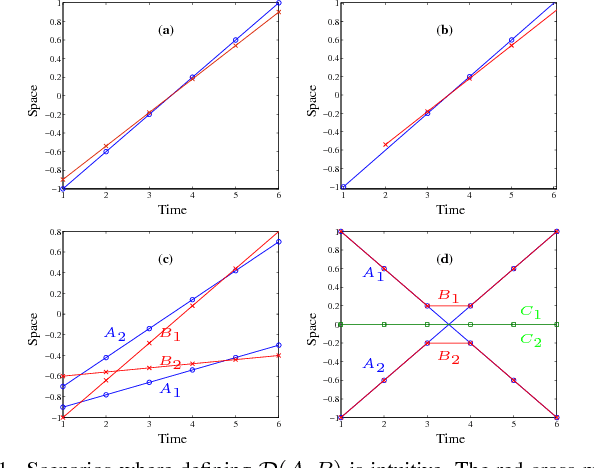
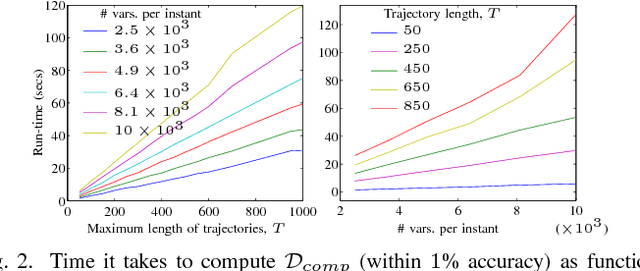
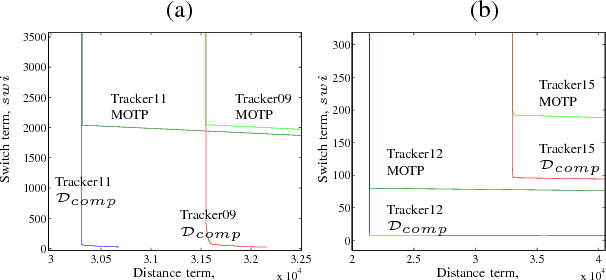
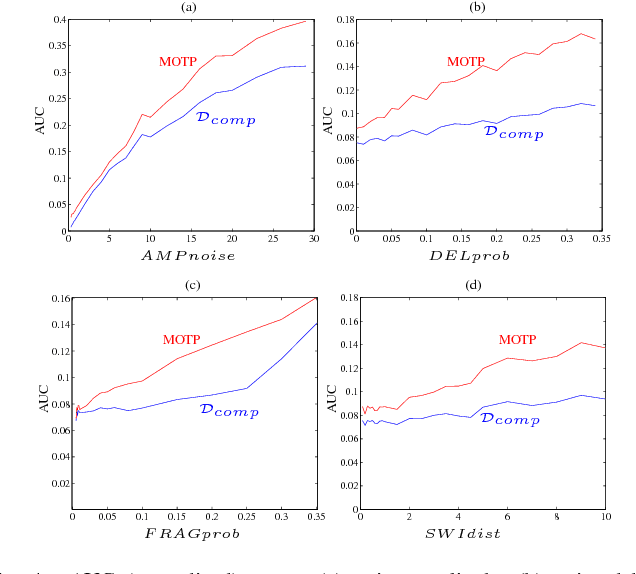
A metric for sets of trajectories that is practical and mathematically consistent

Metrics on the space of sets of trajectories are important for scientists in the field of computer vision, machine learning, robotics, and general artificial intelligence. However, existing notions of closeness between sets of trajectories are either mathematically inconsistent or of limited practical use. In this paper, we outline the limitations in the current mathematically-consistent metrics, which are based on OSPA (Schuhmacher et al. 2008); and the inconsistencies in the heuristic notions of closeness used in practice, whose main ideas are common to the CLEAR MOT measures (Keni and Rainer 2008) widely used in computer vision. In two steps, we then propose a new intuitive metric between sets of trajectories and address these limitations. First, we explain a solution that leads to a metric that is hard to compute. Then we modify this formulation to obtain a metric that is easy to compute while keeping the useful properties of the previous metric. Our notion of closeness is the first demonstrating the following three features: the metric 1) can be quickly computed, 2) incorporates confusion of trajectories' identity in an optimal way, and 3) is a metric in the mathematical sense.

Tuning Over-Relaxed ADMM

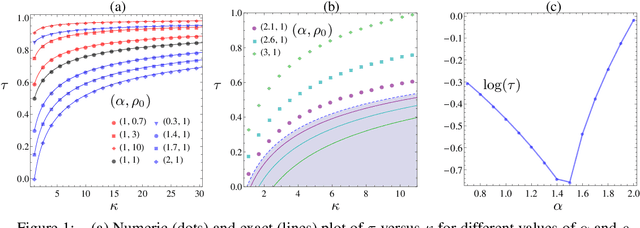
The framework of Integral Quadratic Constraints (IQC) reduces the computation of upper bounds on the convergence rate of several optimization algorithms to a semi-definite program (SDP). In the case of over-relaxed Alternating Direction Method of Multipliers (ADMM), an explicit and closed form solution to this SDP was derived in our recent work [1]. The purpose of this paper is twofold. First, we summarize these results. Second, we explore one of its consequences which allows us to obtain general and simple formulas for optimal parameter selection. These results are valid for arbitrary strongly convex objective functions.

An Explicit Rate Bound for the Over-Relaxed ADMM

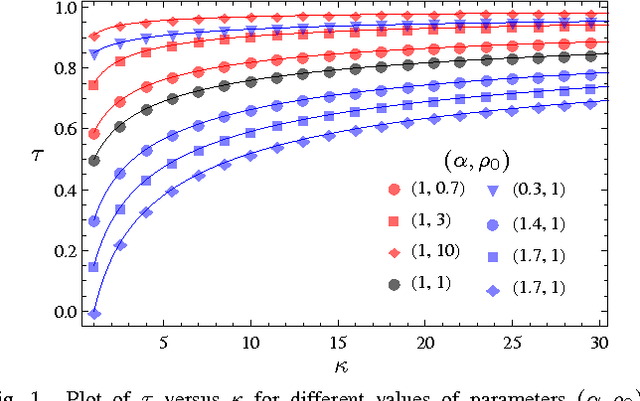
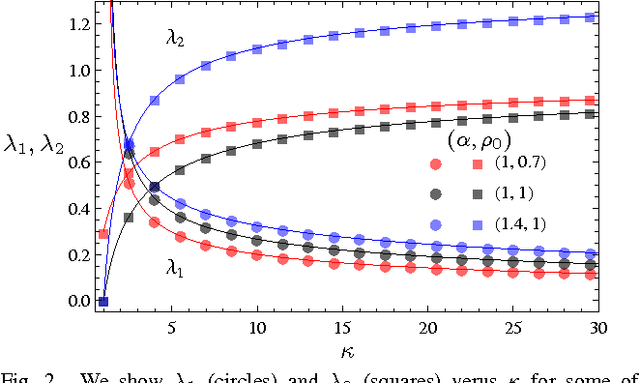
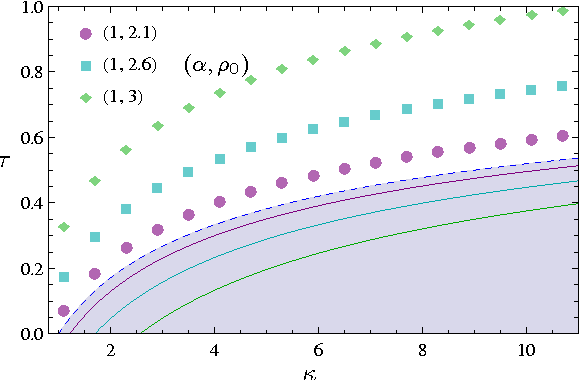
The framework of Integral Quadratic Constraints of Lessard et al. (2014) reduces the computation of upper bounds on the convergence rate of several optimization algorithms to semi-definite programming (SDP). Followup work by Nishihara et al. (2015) applies this technique to the entire family of over-relaxed Alternating Direction Method of Multipliers (ADMM). Unfortunately, they only provide an explicit error bound for sufficiently large values of some of the parameters of the problem, leaving the computation for the general case as a numerical optimization problem. In this paper we provide an exact analytical solution to this SDP and obtain a general and explicit upper bound on the convergence rate of the entire family of over-relaxed ADMM. Furthermore, we demonstrate that it is not possible to extract from this SDP a general bound better than ours. We end with a few numerical illustrations of our result and a comparison between the convergence rate we obtain for the ADMM with known convergence rates for the Gradient Descent.

An Explicit Convergence Rate for Nesterov's Method from SDP

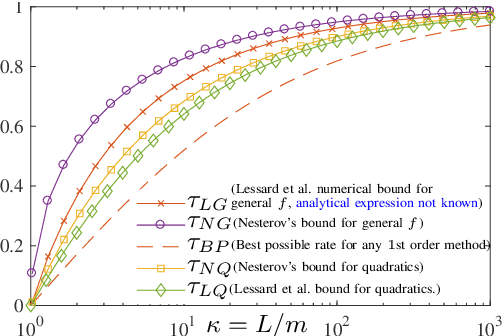
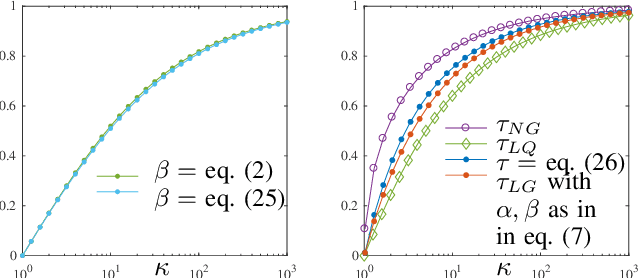
The framework of Integral Quadratic Constraints (IQC) introduced by Lessard et al. (2014) reduces the computation of upper bounds on the convergence rate of several optimization algorithms to semi-definite programming (SDP). In particular, this technique was applied to Nesterov's accelerated method (NAM). For quadratic functions, this SDP was explicitly solved leading to a new bound on the convergence rate of NAM, and for arbitrary strongly convex functions it was shown numerically that IQC can improve bounds from Nesterov (2004). Unfortunately, an explicit analytic solution to the SDP was not provided. In this paper, we provide such an analytical solution, obtaining a new general and explicit upper bound on the convergence rate of NAM, which we further optimize over its parameters. To the best of our knowledge, this is the best, and explicit, upper bound on the convergence rate of NAM for strongly convex functions.

Generative Adversarial Active Learning

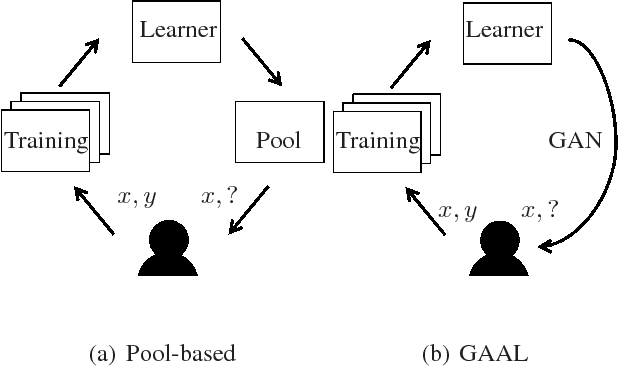
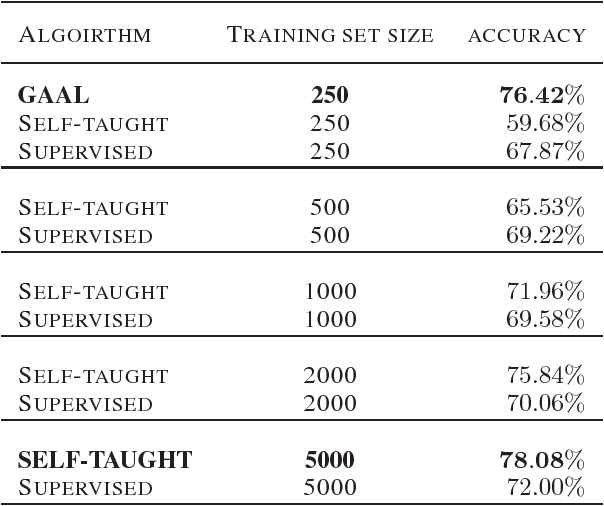
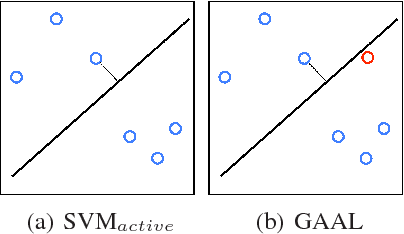
We propose a new active learning by query synthesis approach using Generative Adversarial Networks (GAN). Different from regular active learning, the resulting algorithm adaptively synthesizes training instances for querying to increase learning speed. We generate queries according to the uncertainty principle, but our idea can work with other active learning principles. We report results from various numerical experiments to demonstrate the effectiveness the proposed approach. In some settings, the proposed algorithm outperforms traditional pool-based approaches. To the best our knowledge, this is the first active learning work using GAN.