A metric for sets of trajectories that is practical and mathematically consistent
Paper and Code
Mar 06, 2018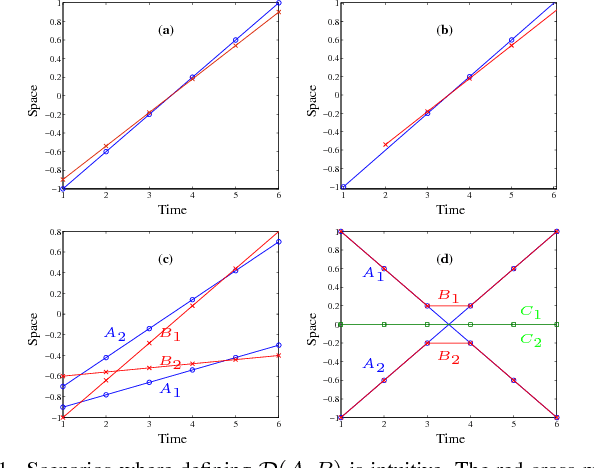
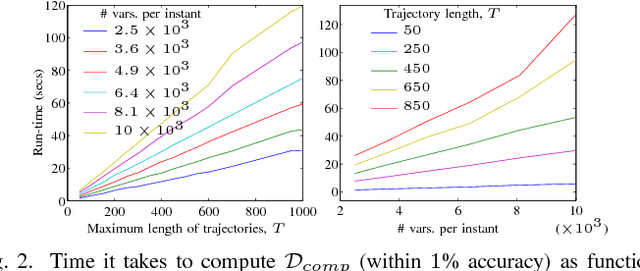
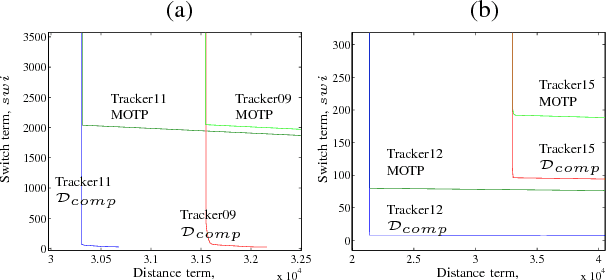
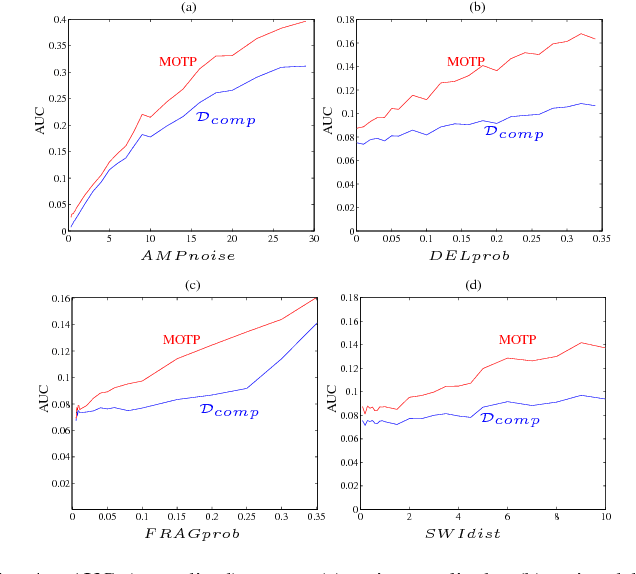
Metrics on the space of sets of trajectories are important for scientists in the field of computer vision, machine learning, robotics, and general artificial intelligence. However, existing notions of closeness between sets of trajectories are either mathematically inconsistent or of limited practical use. In this paper, we outline the limitations in the current mathematically-consistent metrics, which are based on OSPA (Schuhmacher et al. 2008); and the inconsistencies in the heuristic notions of closeness used in practice, whose main ideas are common to the CLEAR MOT measures (Keni and Rainer 2008) widely used in computer vision. In two steps, we then propose a new intuitive metric between sets of trajectories and address these limitations. First, we explain a solution that leads to a metric that is hard to compute. Then we modify this formulation to obtain a metric that is easy to compute while keeping the useful properties of the previous metric. Our notion of closeness is the first demonstrating the following three features: the metric 1) can be quickly computed, 2) incorporates confusion of trajectories' identity in an optimal way, and 3) is a metric in the mathematical sense.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge