An Explicit Convergence Rate for Nesterov's Method from SDP

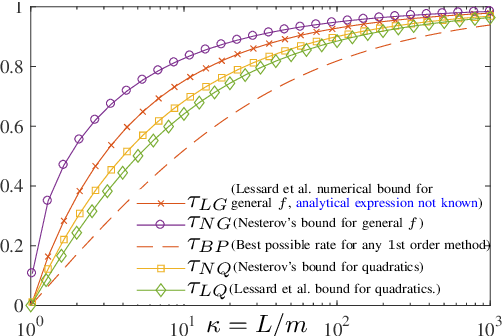
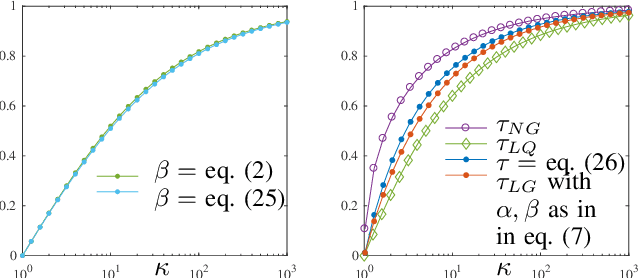
The framework of Integral Quadratic Constraints (IQC) introduced by Lessard et al. (2014) reduces the computation of upper bounds on the convergence rate of several optimization algorithms to semi-definite programming (SDP). In particular, this technique was applied to Nesterov's accelerated method (NAM). For quadratic functions, this SDP was explicitly solved leading to a new bound on the convergence rate of NAM, and for arbitrary strongly convex functions it was shown numerically that IQC can improve bounds from Nesterov (2004). Unfortunately, an explicit analytic solution to the SDP was not provided. In this paper, we provide such an analytical solution, obtaining a new general and explicit upper bound on the convergence rate of NAM, which we further optimize over its parameters. To the best of our knowledge, this is the best, and explicit, upper bound on the convergence rate of NAM for strongly convex functions.

Aggressive Sampling for Multi-class to Binary Reduction with Applications to Text Classification

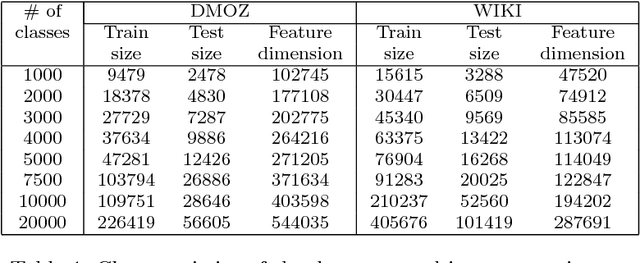
We address the problem of multi-class classification in the case where the number of classes is very large. We propose a double sampling strategy on top of a multi-class to binary reduction strategy, which transforms the original multi-class problem into a binary classification problem over pairs of examples. The aim of the sampling strategy is to overcome the curse of long-tailed class distributions exhibited in majority of large-scale multi-class classification problems and to reduce the number of pairs of examples in the expanded data. We show that this strategy does not alter the consistency of the empirical risk minimization principle defined over the double sample reduction. Experiments are carried out on DMOZ and Wikipedia collections with 10,000 to 100,000 classes where we show the efficiency of the proposed approach in terms of training and prediction time, memory consumption, and predictive performance with respect to state-of-the-art approaches.

An Asynchronous Distributed Framework for Large-scale Learning Based on Parameter Exchanges

In many distributed learning problems, the heterogeneous loading of computing machines may harm the overall performance of synchronous strategies. In this paper, we propose an effective asynchronous distributed framework for the minimization of a sum of smooth functions, where each machine performs iterations in parallel on its local function and updates a shared parameter asynchronously. In this way, all machines can continuously work even though they do not have the latest version of the shared parameter. We prove the convergence of the consistency of this general distributed asynchronous method for gradient iterations then show its efficiency on the matrix factorization problem for recommender systems and on binary classification.