Exact inference under the perfect phylogeny model

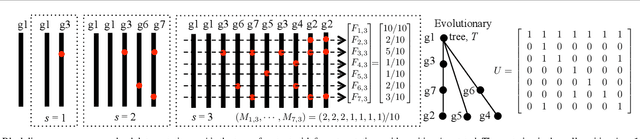
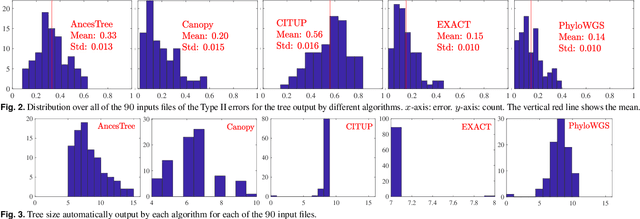
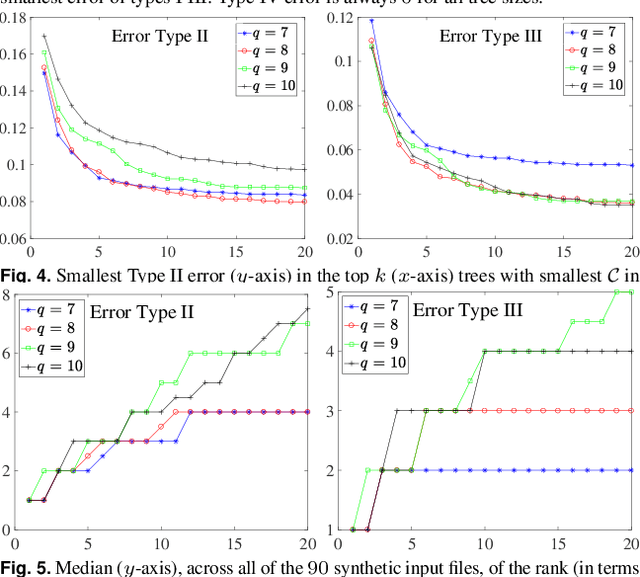
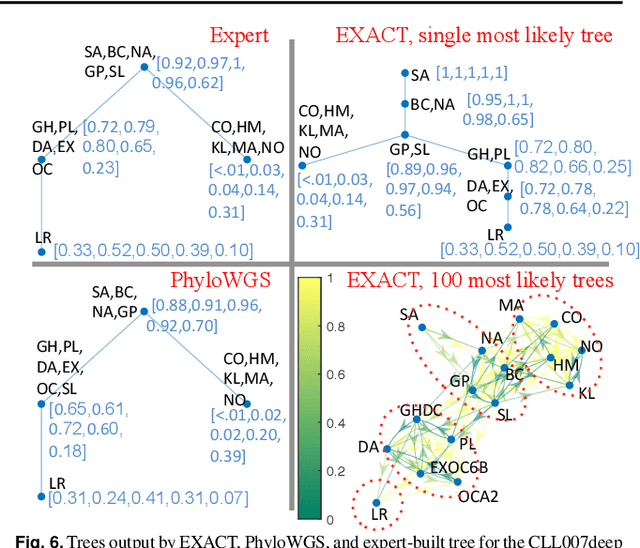
Motivation: Many inference tools use the Perfect Phylogeny Model (PPM) to learn trees from noisy variant allele frequency (VAF) data. Learning in this setting is hard, and existing tools use approximate or heuristic algorithms. An algorithmic improvement is important to help disentangle the limitations of the PPM's assumptions from the limitations in our capacity to learn under it. Results: We make such improvement in the scenario, where the mutations that are relevant for evolution can be clustered into a small number of groups, and the trees to be reconstructed have a small number of nodes. We use a careful combination of algorithms, software, and hardware, to develop EXACT: a tool that can explore the space of all possible phylogenetic trees, and performs exact inference under the PPM with noisy data. EXACT allows users to obtain not just the most-likely tree for some input data, but exact statistics about the distribution of trees that might explain the data. We show that EXACT outperforms several existing tools for this same task. Availability: https://github.com/surjray-repos/EXACT

How should we (correctly) compare multiple graphs?

Graphs are used in almost every scientific discipline to express relations among a set of objects. Algorithms that compare graphs, and output a closeness score, or a correspondence among their nodes, are thus extremely important. Despite the large amount of work done, many of the scalable algorithms to compare graphs do not produce closeness scores that satisfy the intuitive properties of metrics. This is problematic since non-metrics are known to degrade the performance of algorithms such as distance-based clustering of graphs (Stratis et al. 2018). On the other hand, the use of metrics increases the performance of several machine learning tasks (Indyk et al. 1999, Clarkson et al. 1999, Angiulli et al. 2002 and Ackermann et al, 2010). In this paper, we introduce a new family of multi-distances (a distance between more than two elements) that satisfies a generalization of the properties of metrics to multiple elements. In the context of comparing graphs, we are the first to show the existence of multi-distances that simultaneously incorporate the useful property of alignment consistency (Nguyen et al. 2011), and a generalized metric property, and that can be computed via convex optimization.

An Explicit Convergence Rate for Nesterov's Method from SDP

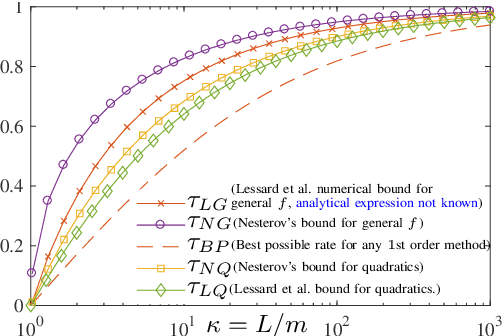
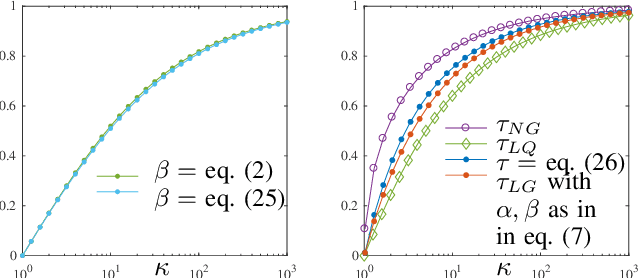
The framework of Integral Quadratic Constraints (IQC) introduced by Lessard et al. (2014) reduces the computation of upper bounds on the convergence rate of several optimization algorithms to semi-definite programming (SDP). In particular, this technique was applied to Nesterov's accelerated method (NAM). For quadratic functions, this SDP was explicitly solved leading to a new bound on the convergence rate of NAM, and for arbitrary strongly convex functions it was shown numerically that IQC can improve bounds from Nesterov (2004). Unfortunately, an explicit analytic solution to the SDP was not provided. In this paper, we provide such an analytical solution, obtaining a new general and explicit upper bound on the convergence rate of NAM, which we further optimize over its parameters. To the best of our knowledge, this is the best, and explicit, upper bound on the convergence rate of NAM for strongly convex functions.

An opportunistic linear-convex algorithm for localization in mobile robot networks

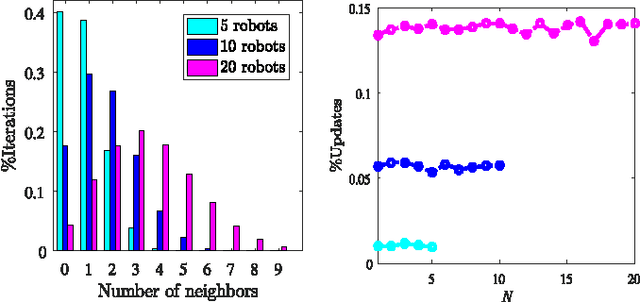
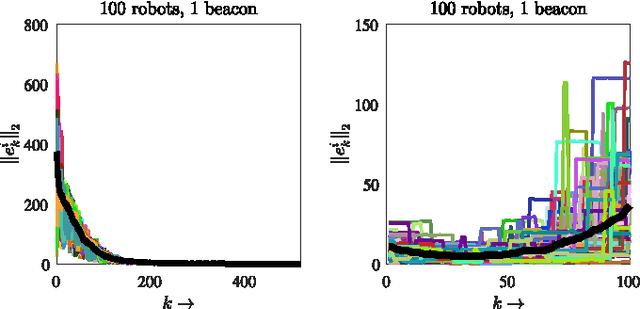
In this paper, we develop a \textcolor{black}{\emph{distributed}} algorithm to localize a network of robots moving arbitrarily in a bounded region. In the case of such mobile networks, the main challenge is that the robots may not be able to find nearby robots to implement a distributed algorithm. We address this issue by providing an opportunistic algorithm that only implements a location update when there are nearby robots and does not update otherwise. We assume that each robot measures a noisy version of its motion and the distances to the nearby robots. To localize a network of mobile robots in~$\mathbb{R}^m$, we provide a simple \emph{linear} update, which is based on barycentric coordinates and is linear-convex. We abstract the corresponding localization algorithm as a Linear Time-Varying (LTV) system and show that it asymptotically converges to the true locations~of~the robots. We first focus on the noiseless case, where the distance and motion vectors are known (measured) perfectly, and provide sufficient conditions on the convergence of the algorithm. We then evaluate the performance of the algorithm in the presence of noise and provide modifications to counter the undesirable effects of noise. \textcolor{black}{We further show that our algorithm precisely tracks a mobile network as long as there is at least one known beacon (a node whose location is perfectly known).