An opportunistic linear-convex algorithm for localization in mobile robot networks
Paper and Code
Mar 19, 2017
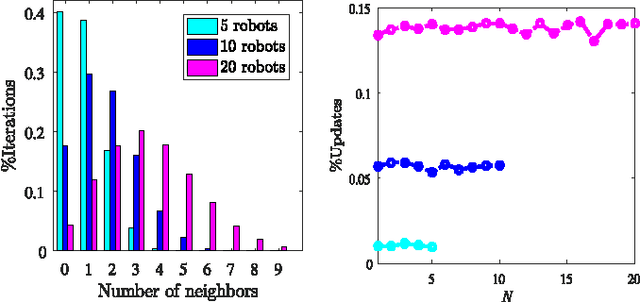
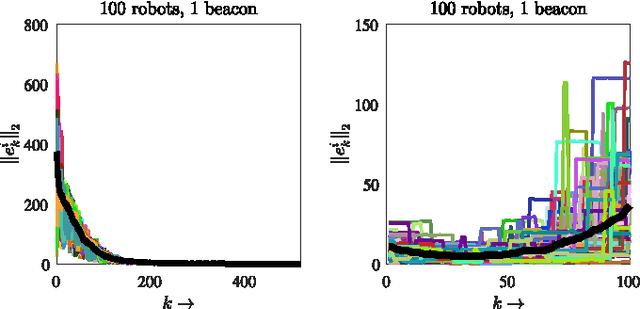

In this paper, we develop a \textcolor{black}{\emph{distributed}} algorithm to localize a network of robots moving arbitrarily in a bounded region. In the case of such mobile networks, the main challenge is that the robots may not be able to find nearby robots to implement a distributed algorithm. We address this issue by providing an opportunistic algorithm that only implements a location update when there are nearby robots and does not update otherwise. We assume that each robot measures a noisy version of its motion and the distances to the nearby robots. To localize a network of mobile robots in~$\mathbb{R}^m$, we provide a simple \emph{linear} update, which is based on barycentric coordinates and is linear-convex. We abstract the corresponding localization algorithm as a Linear Time-Varying (LTV) system and show that it asymptotically converges to the true locations~of~the robots. We first focus on the noiseless case, where the distance and motion vectors are known (measured) perfectly, and provide sufficient conditions on the convergence of the algorithm. We then evaluate the performance of the algorithm in the presence of noise and provide modifications to counter the undesirable effects of noise. \textcolor{black}{We further show that our algorithm precisely tracks a mobile network as long as there is at least one known beacon (a node whose location is perfectly known).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge