Variational Wasserstein Barycenters for Geometric Clustering

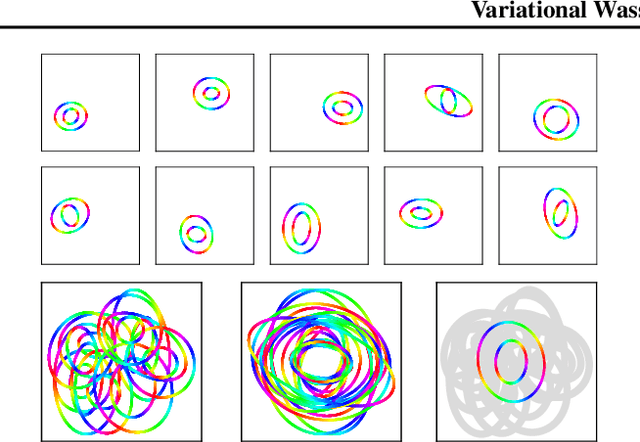
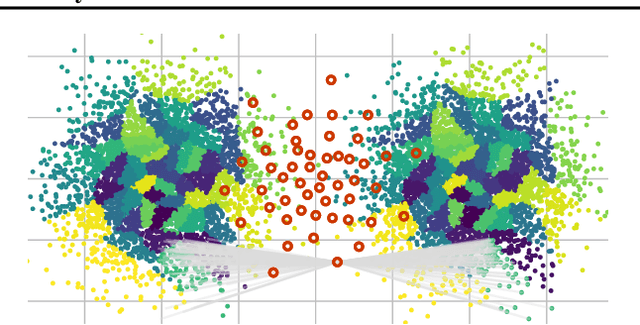
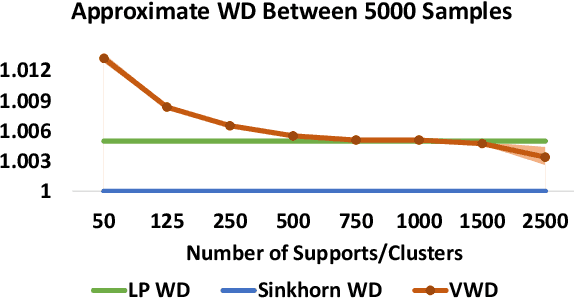
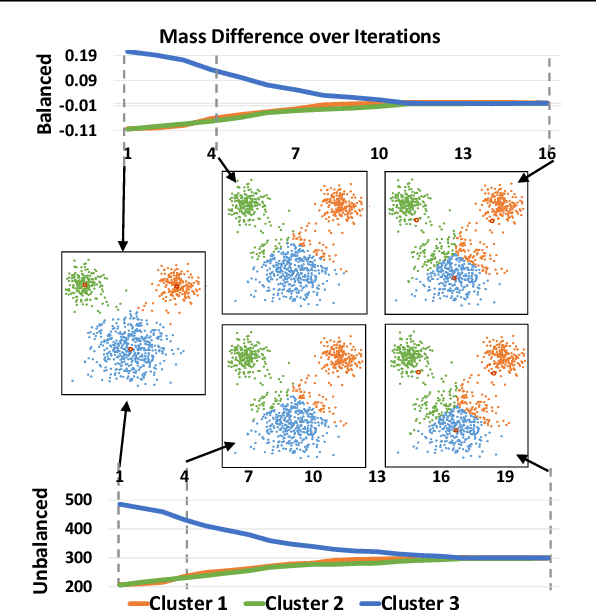
We propose to compute Wasserstein barycenters (WBs) by solving for Monge maps with variational principle. We discuss the metric properties of WBs and explore their connections, especially the connections of Monge WBs, to K-means clustering and co-clustering. We also discuss the feasibility of Monge WBs on unbalanced measures and spherical domains. We propose two new problems -- regularized K-means and Wasserstein barycenter compression. We demonstrate the use of VWBs in solving these clustering-related problems.

How should we (correctly) compare multiple graphs?

Graphs are used in almost every scientific discipline to express relations among a set of objects. Algorithms that compare graphs, and output a closeness score, or a correspondence among their nodes, are thus extremely important. Despite the large amount of work done, many of the scalable algorithms to compare graphs do not produce closeness scores that satisfy the intuitive properties of metrics. This is problematic since non-metrics are known to degrade the performance of algorithms such as distance-based clustering of graphs (Stratis et al. 2018). On the other hand, the use of metrics increases the performance of several machine learning tasks (Indyk et al. 1999, Clarkson et al. 1999, Angiulli et al. 2002 and Ackermann et al, 2010). In this paper, we introduce a new family of multi-distances (a distance between more than two elements) that satisfies a generalization of the properties of metrics to multiple elements. In the context of comparing graphs, we are the first to show the existence of multi-distances that simultaneously incorporate the useful property of alignment consistency (Nguyen et al. 2011), and a generalized metric property, and that can be computed via convex optimization.

On the Complexity of the Weighted Fused Lasso

The solution path of the 1D fused lasso for an $n$-dimensional input is piecewise linear with $\mathcal{O}(n)$ segments (Hoefling et al. 2010 and Tibshirani et al 2011). However, existing proofs of this bound do not hold for the weighted fused lasso. At the same time, results for the generalized lasso, of which the weighted fused lasso is a special case, allow $\Omega(3^n)$ segments (Mairal et al. 2012). In this paper, we prove that the number of segments in the solution path of the weighted fused lasso is $\mathcal{O}(n^2)$, and that, for some instances, it is $\Omega(n^2)$. We also give a new, very simple, proof of the $\mathcal{O}(n)$ bound for the fused lasso.

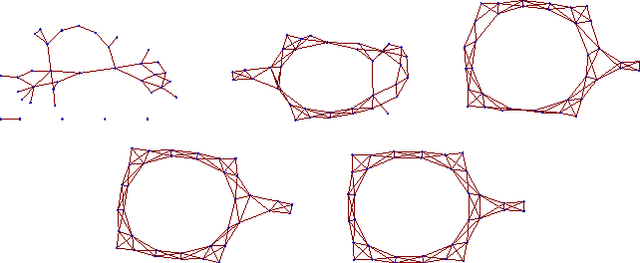
A message-passing algorithm for multi-agent trajectory planning

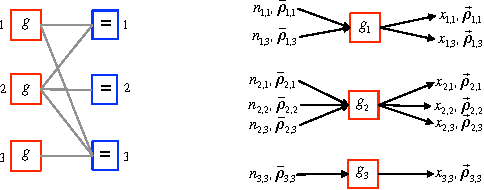
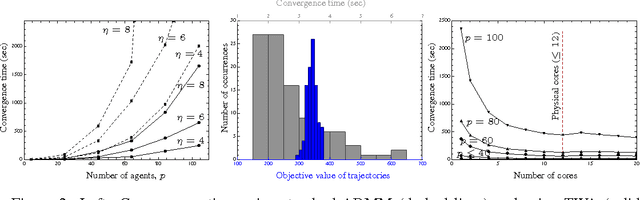
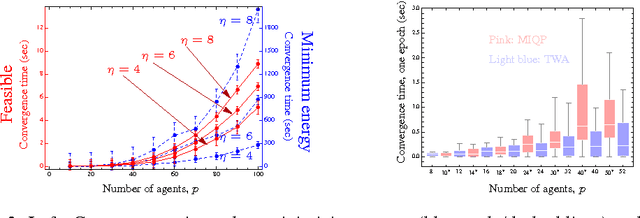
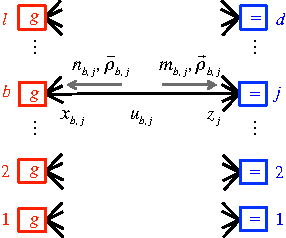
We describe a novel approach for computing collision-free \emph{global} trajectories for $p$ agents with specified initial and final configurations, based on an improved version of the alternating direction method of multipliers (ADMM). Compared with existing methods, our approach is naturally parallelizable and allows for incorporating different cost functionals with only minor adjustments. We apply our method to classical challenging instances and observe that its computational requirements scale well with $p$ for several cost functionals. We also show that a specialization of our algorithm can be used for {\em local} motion planning by solving the problem of joint optimization in velocity space.

Support Recovery for the Drift Coefficient of High-Dimensional Diffusions

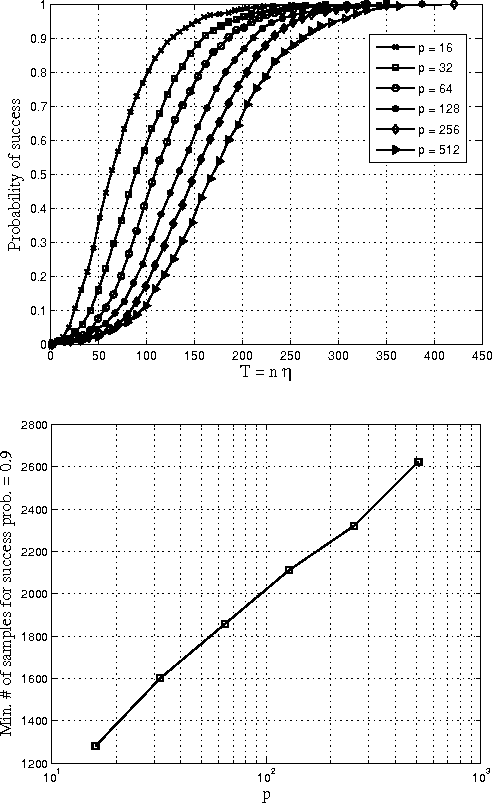
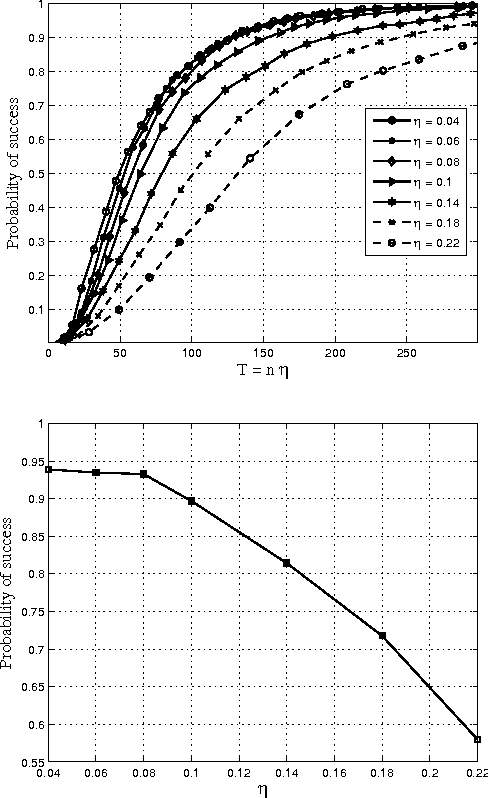
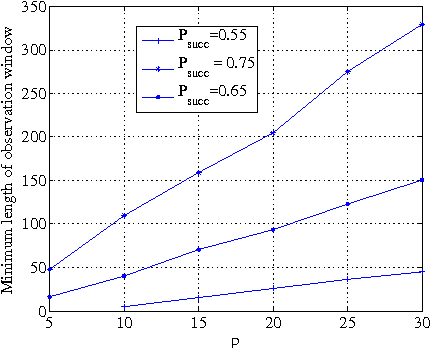
Consider the problem of learning the drift coefficient of a $p$-dimensional stochastic differential equation from a sample path of length $T$. We assume that the drift is parametrized by a high-dimensional vector, and study the support recovery problem when both $p$ and $T$ can tend to infinity. In particular, we prove a general lower bound on the sample-complexity $T$ by using a characterization of mutual information as a time integral of conditional variance, due to Kadota, Zakai, and Ziv. For linear stochastic differential equations, the drift coefficient is parametrized by a $p\times p$ matrix which describes which degrees of freedom interact under the dynamics. In this case, we analyze a $\ell_1$-regularized least squares estimator and prove an upper bound on $T$ that nearly matches the lower bound on specific classes of sparse matrices.

Which graphical models are difficult to learn?

We consider the problem of learning the structure of Ising models (pairwise binary Markov random fields) from i.i.d. samples. While several methods have been proposed to accomplish this task, their relative merits and limitations remain somewhat obscure. By analyzing a number of concrete examples, we show that low-complexity algorithms systematically fail when the Markov random field develops long-range correlations. More precisely, this phenomenon appears to be related to the Ising model phase transition (although it does not coincide with it).