Support Recovery for the Drift Coefficient of High-Dimensional Diffusions
Paper and Code
Aug 20, 2013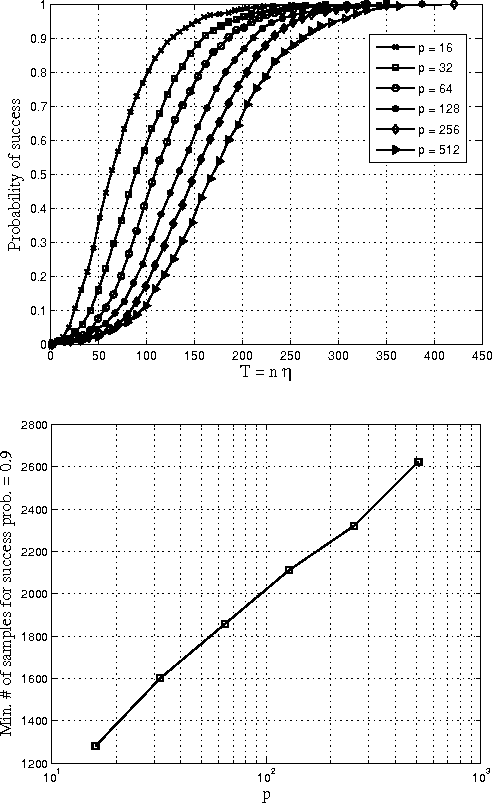
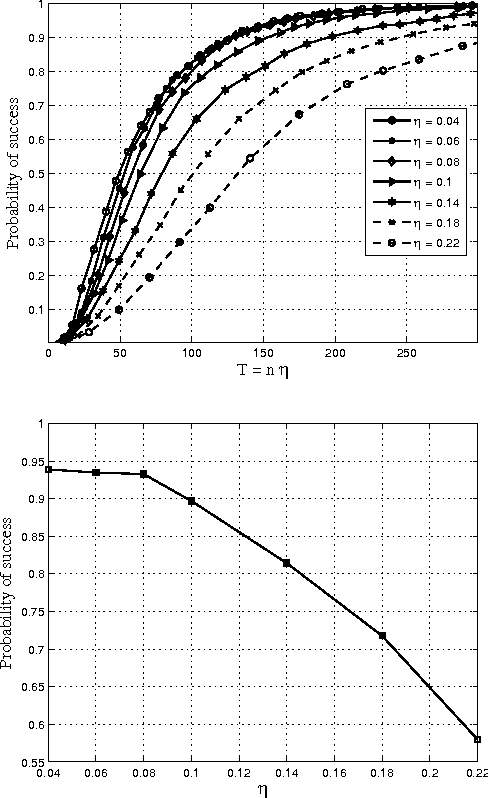
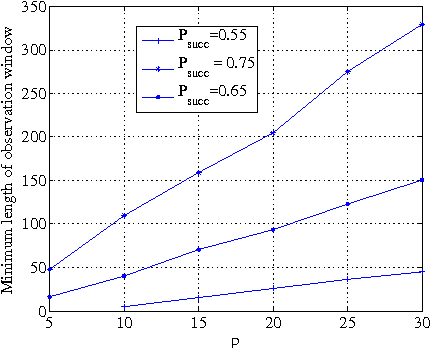
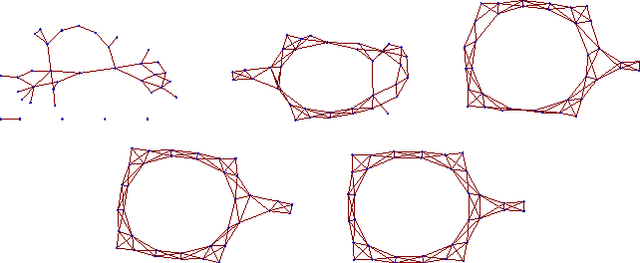
Consider the problem of learning the drift coefficient of a $p$-dimensional stochastic differential equation from a sample path of length $T$. We assume that the drift is parametrized by a high-dimensional vector, and study the support recovery problem when both $p$ and $T$ can tend to infinity. In particular, we prove a general lower bound on the sample-complexity $T$ by using a characterization of mutual information as a time integral of conditional variance, due to Kadota, Zakai, and Ziv. For linear stochastic differential equations, the drift coefficient is parametrized by a $p\times p$ matrix which describes which degrees of freedom interact under the dynamics. In this case, we analyze a $\ell_1$-regularized least squares estimator and prove an upper bound on $T$ that nearly matches the lower bound on specific classes of sparse matrices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge