Jonathan Yedidia
Self-Play Learning Without a Reward Metric
Dec 16, 2019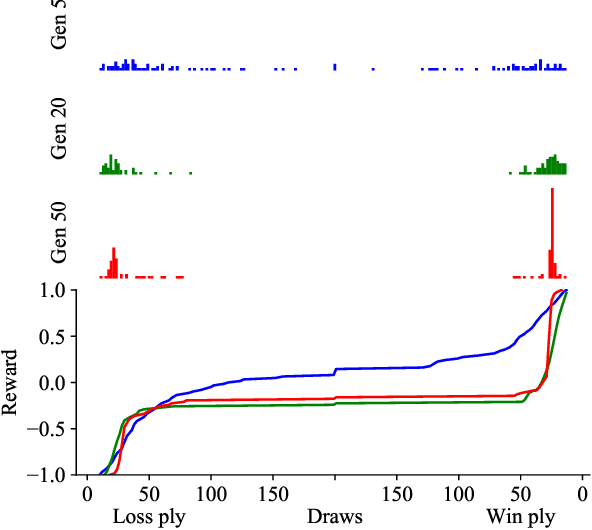
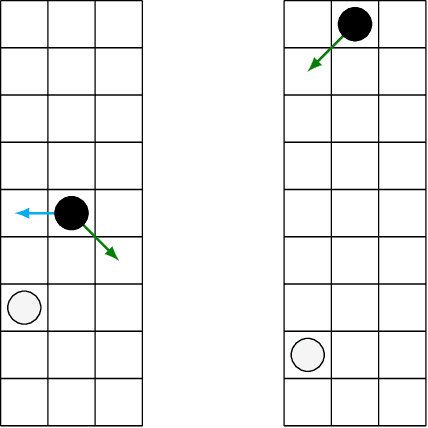

Abstract:The AlphaZero algorithm for the learning of strategy games via self-play, which has produced superhuman ability in the games of Go, chess, and shogi, uses a quantitative reward function for game outcomes, requiring the users of the algorithm to explicitly balance different components of the reward against each other, such as the game winner and margin of victory. We present a modification to the AlphaZero algorithm that requires only a total ordering over game outcomes, obviating the need to perform any quantitative balancing of reward components. We demonstrate that this system learns optimal play in a comparable amount of time to AlphaZero on a sample game.
Monotone Learning with Rectified Wire Networks
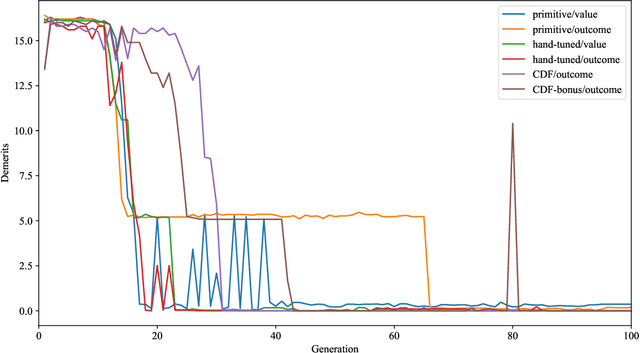
Aug 24, 2018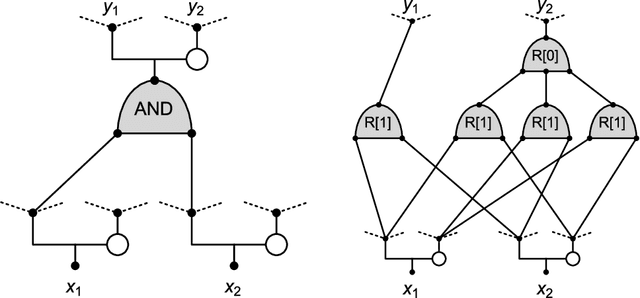

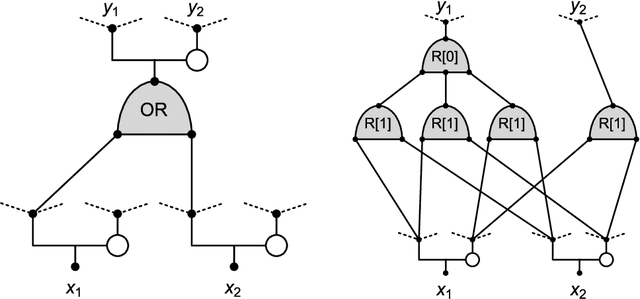

Abstract:We introduce a new neural network model, together with a tractable and monotone online learning algorithm. Our model describes feed-forward networks for classification, with one output node for each class. The only nonlinear operation is rectification using a ReLU function with a bias. However, there is a rectifier on every edge rather than at the nodes of the network. There are also weights, but these are positive, static, and associated with the nodes. Our "rectified wire" networks are able to represent arbitrary Boolean functions. Only the bias parameters, on the edges of the network, are learned. Another departure in our approach, from standard neural networks, is that the loss function is replaced by a constraint. This constraint is simply that the value of the output node associated with the correct class should be zero. Our model has the property that the exact norm-minimizing parameter update, required to correctly classify a training item, is the solution to a quadratic program that can be computed with a few passes through the network. We demonstrate a training algorithm using this update, called sequential deactivation (SDA), on MNIST and some synthetic datasets. Upon adopting a natural choice for the nodal weights, SDA has no hyperparameters other than those describing the network structure. Our experiments explore behavior with respect to network size and depth in a family of sparse expander networks.
Proactive Message Passing on Memory Factor Networks
Jan 18, 2016



Abstract:We introduce a new type of graphical model that we call a "memory factor network" (MFN). We show how to use MFNs to model the structure inherent in many types of data sets. We also introduce an associated message-passing style algorithm called "proactive message passing"' (PMP) that performs inference on MFNs. PMP comes with convergence guarantees and is efficient in comparison to competing algorithms such as variants of belief propagation. We specialize MFNs and PMP to a number of distinct types of data (discrete, continuous, labelled) and inference problems (interpolation, hypothesis testing), provide examples, and discuss approaches for efficient implementation.
The Boundary Forest Algorithm for Online Supervised and Unsupervised Learning
May 12, 2015



Abstract:We describe a new instance-based learning algorithm called the Boundary Forest (BF) algorithm, that can be used for supervised and unsupervised learning. The algorithm builds a forest of trees whose nodes store previously seen examples. It can be shown data points one at a time and updates itself incrementally, hence it is naturally online. Few instance-based algorithms have this property while being simultaneously fast, which the BF is. This is crucial for applications where one needs to respond to input data in real time. The number of children of each node is not set beforehand but obtained from the training procedure, which makes the algorithm very flexible with regards to what data manifolds it can learn. We test its generalization performance and speed on a range of benchmark datasets and detail in which settings it outperforms the state of the art. Empirically we find that training time scales as O(DNlog(N)) and testing as O(Dlog(N)), where D is the dimensionality and N the amount of data,
* 7 pages, 4 figs, 1 page supp. info
A message-passing algorithm for multi-agent trajectory planning
Nov 18, 2013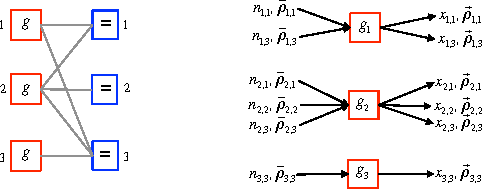
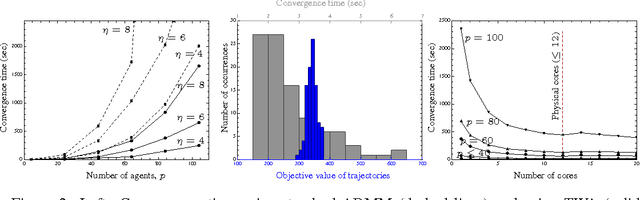
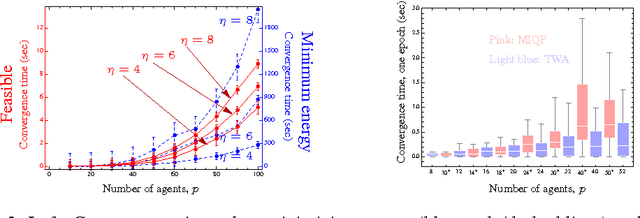
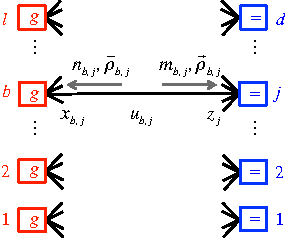
Abstract:We describe a novel approach for computing collision-free \emph{global} trajectories for $p$ agents with specified initial and final configurations, based on an improved version of the alternating direction method of multipliers (ADMM). Compared with existing methods, our approach is naturally parallelizable and allows for incorporating different cost functionals with only minor adjustments. We apply our method to classical challenging instances and observe that its computational requirements scale well with $p$ for several cost functionals. We also show that a specialization of our algorithm can be used for {\em local} motion planning by solving the problem of joint optimization in velocity space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge