Jonathan S. Rosenfeld
Cliff-Learning
Feb 14, 2023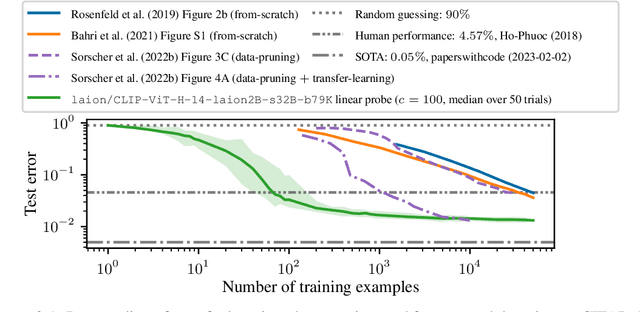
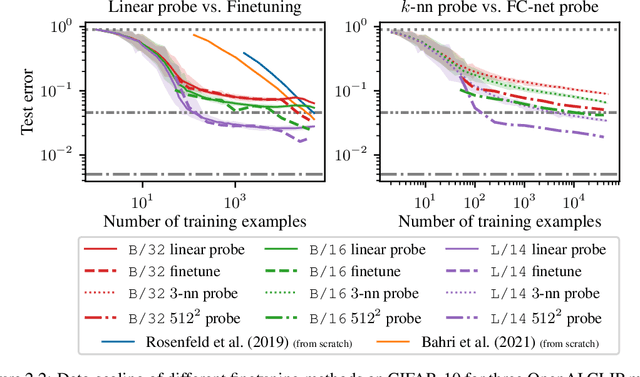
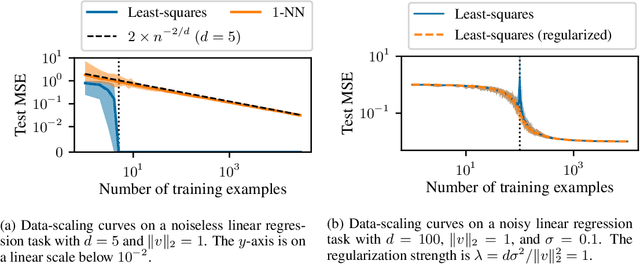
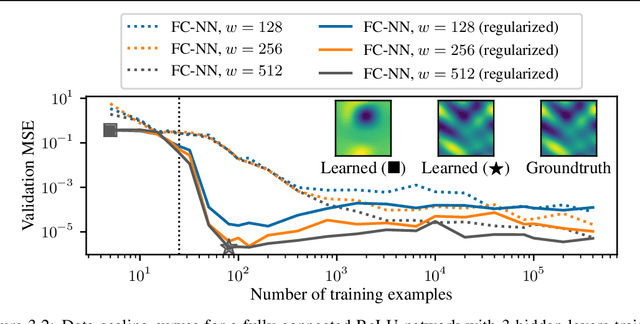
Abstract:We study the data-scaling of transfer learning from foundation models in the low-downstream-data regime. We observe an intriguing phenomenon which we call cliff-learning. Cliff-learning refers to regions of data-scaling laws where performance improves at a faster than power law rate (i.e. regions of concavity on a log-log scaling plot). We conduct an in-depth investigation of foundation-model cliff-learning and study toy models of the phenomenon. We observe that the degree of cliff-learning reflects the degree of compatibility between the priors of a learning algorithm and the task being learned.
Scaling Laws for Deep Learning
Aug 17, 2021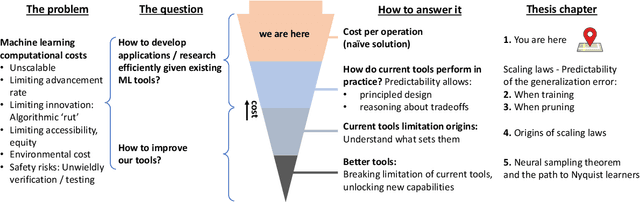
Abstract:Running faster will only get you so far -- it is generally advisable to first understand where the roads lead, then get a car ... The renaissance of machine learning (ML) and deep learning (DL) over the last decade is accompanied by an unscalable computational cost, limiting its advancement and weighing on the field in practice. In this thesis we take a systematic approach to address the algorithmic and methodological limitations at the root of these costs. We first demonstrate that DL training and pruning are predictable and governed by scaling laws -- for state of the art models and tasks, spanning image classification and language modeling, as well as for state of the art model compression via iterative pruning. Predictability, via the establishment of these scaling laws, provides the path for principled design and trade-off reasoning, currently largely lacking in the field. We then continue to analyze the sources of the scaling laws, offering an approximation-theoretic view and showing through the exploration of a noiseless realizable case that DL is in fact dominated by error sources very far from the lower error limit. We conclude by building on the gained theoretical understanding of the scaling laws' origins. We present a conjectural path to eliminate one of the current dominant error sources -- through a data bandwidth limiting hypothesis and the introduction of Nyquist learners -- which can, in principle, reach the generalization error lower limit (e.g. 0 in the noiseless case), at finite dataset size.
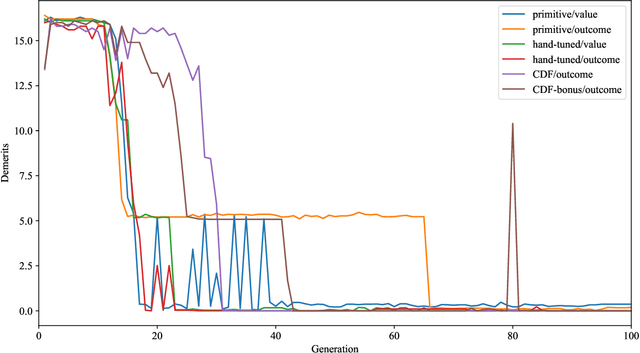
On the Predictability of Pruning Across Scales
Jun 19, 2020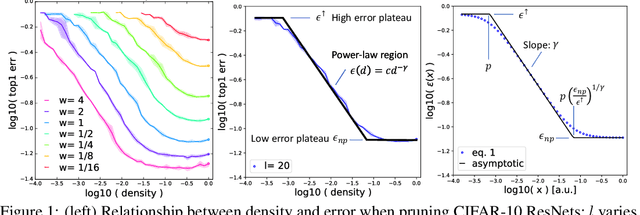
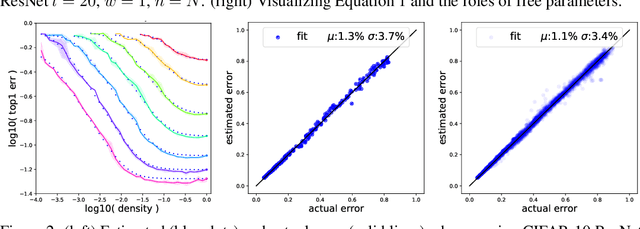
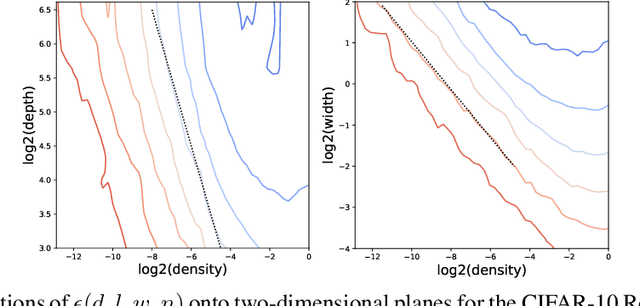
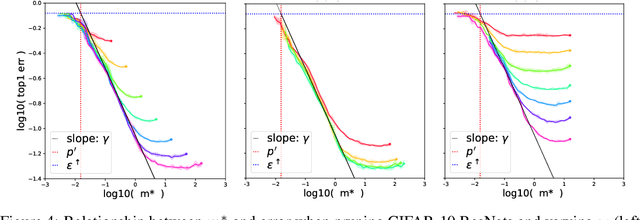
Abstract:We show that the error of magnitude-pruned networks follows a scaling law, and that this law is of a fundamentally different nature than that of unpruned networks. We functionally approximate the error of the pruned networks, showing that it is predictable in terms of an invariant tying width, depth, and pruning level, such that networks of vastly different sparsities are freely interchangeable. We demonstrate the accuracy of this functional approximation over scales spanning orders of magnitude in depth, width, dataset size, and sparsity for CIFAR-10 and ImageNet. As neural networks become ever larger and more expensive to train, our findings enable a framework for reasoning conceptually and analytically about pruning.
Self-Play Learning Without a Reward Metric
Dec 16, 2019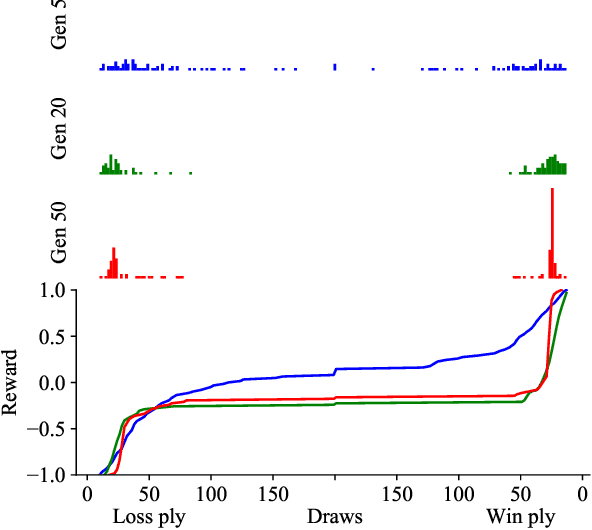
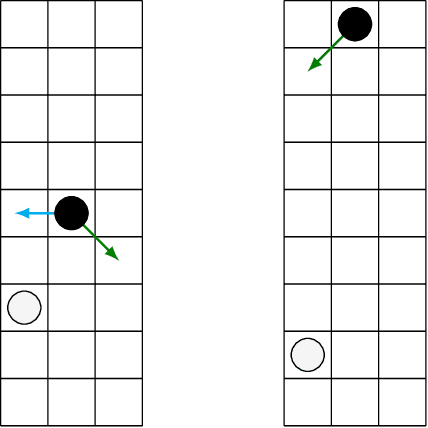

Abstract:The AlphaZero algorithm for the learning of strategy games via self-play, which has produced superhuman ability in the games of Go, chess, and shogi, uses a quantitative reward function for game outcomes, requiring the users of the algorithm to explicitly balance different components of the reward against each other, such as the game winner and margin of victory. We present a modification to the AlphaZero algorithm that requires only a total ordering over game outcomes, obviating the need to perform any quantitative balancing of reward components. We demonstrate that this system learns optimal play in a comparable amount of time to AlphaZero on a sample game.
A Constructive Prediction of the Generalization Error Across Scales
Sep 27, 2019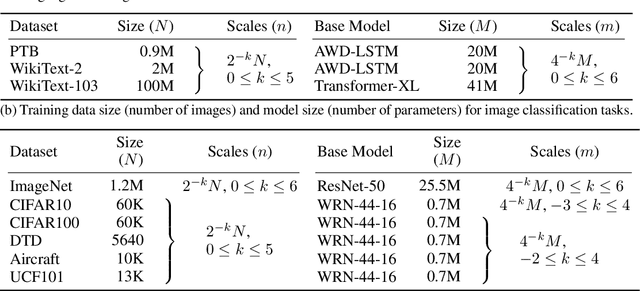
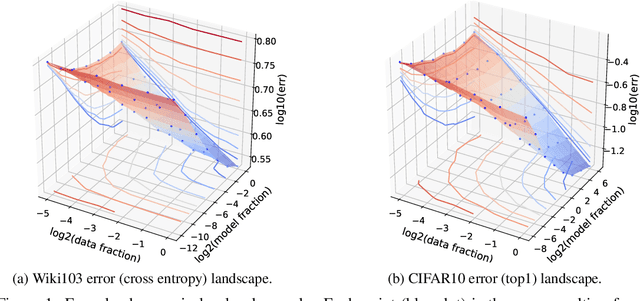
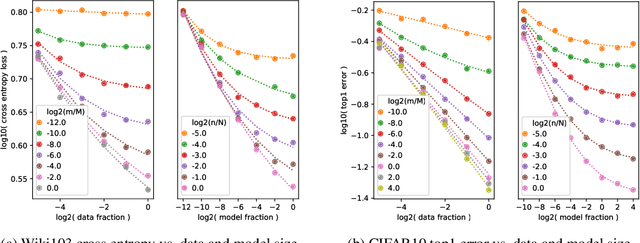
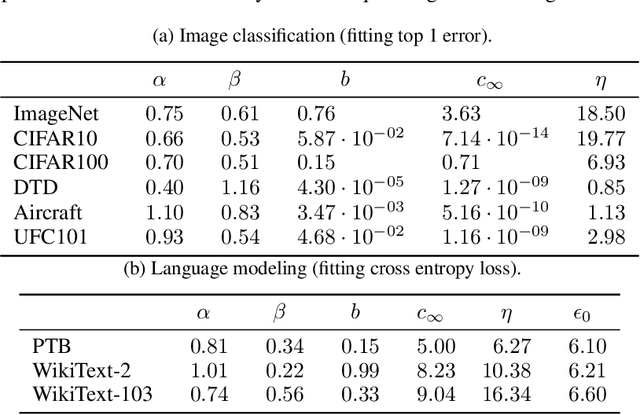
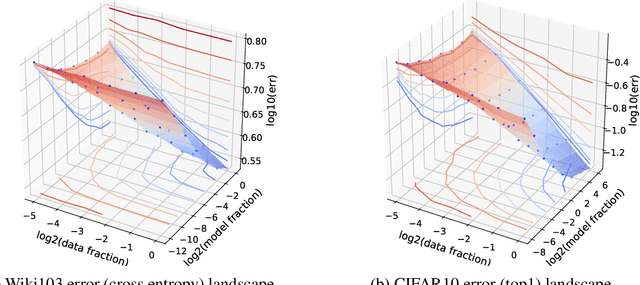
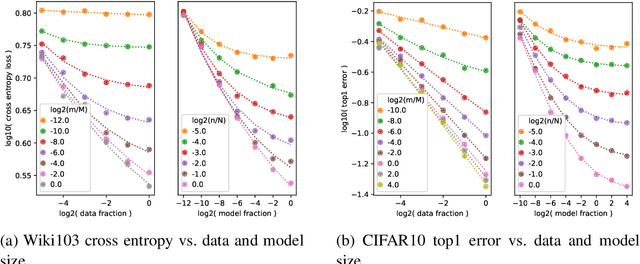
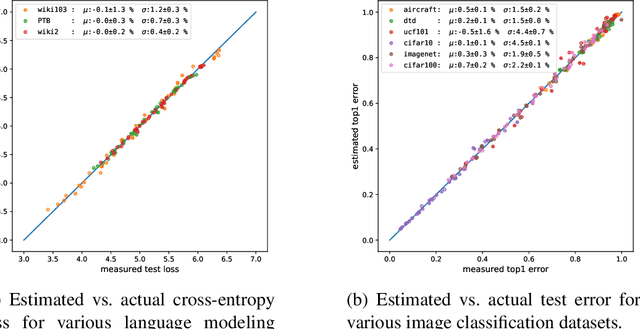
Abstract:The dependency of the generalization error of neural networks on model and dataset size is of critical importance both in practice and for understanding the theory of neural networks. Nevertheless, the functional form of this dependency remains elusive. In this work, we present a functional form which approximates well the generalization error in practice. Capitalizing on the successful concept of model scaling (e.g., width, depth), we are able to simultaneously construct such a form and specify the exact models which can attain it across model/data scales. Our construction follows insights obtained from observations conducted over a range of model/data scales, in various model types and datasets, in vision and language tasks. We show that the form both fits the observations well across scales, and provides accurate predictions from small- to large-scale models and data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge