Self-Play Learning Without a Reward Metric
Paper and Code
Dec 16, 2019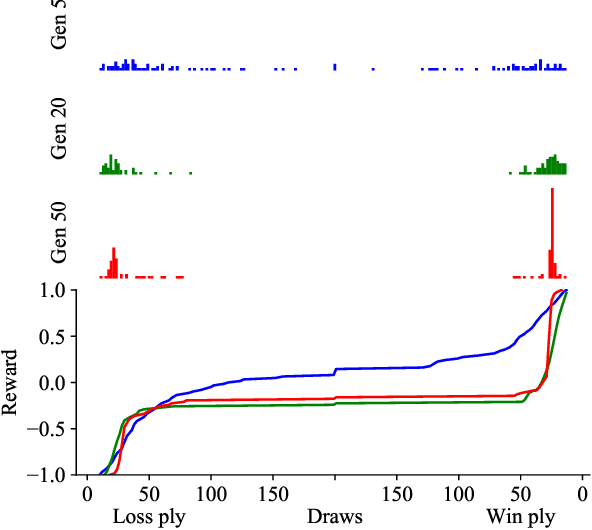
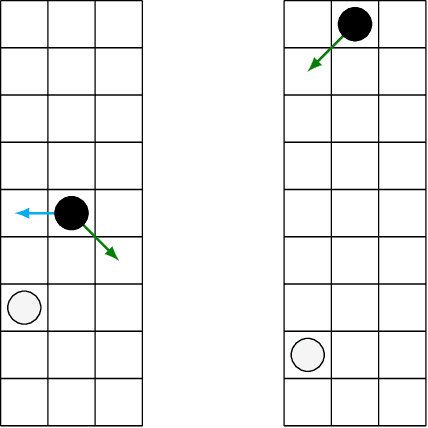
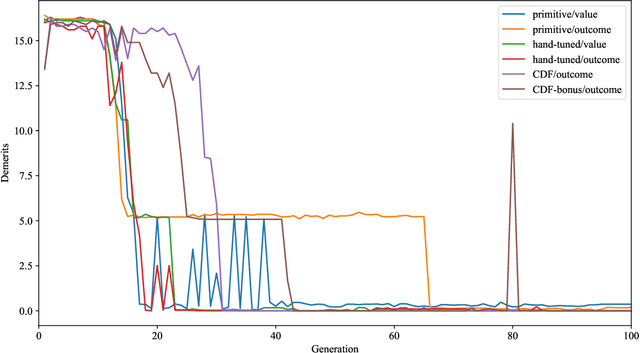

The AlphaZero algorithm for the learning of strategy games via self-play, which has produced superhuman ability in the games of Go, chess, and shogi, uses a quantitative reward function for game outcomes, requiring the users of the algorithm to explicitly balance different components of the reward against each other, such as the game winner and margin of victory. We present a modification to the AlphaZero algorithm that requires only a total ordering over game outcomes, obviating the need to perform any quantitative balancing of reward components. We demonstrate that this system learns optimal play in a comparable amount of time to AlphaZero on a sample game.
* 6 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge