Self-Play Learning Without a Reward Metric

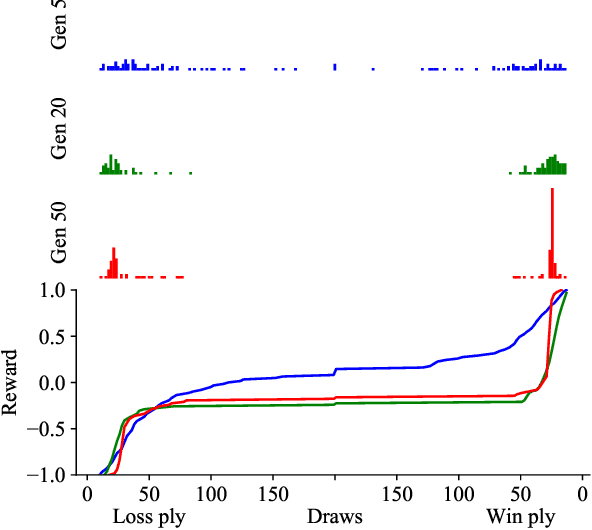
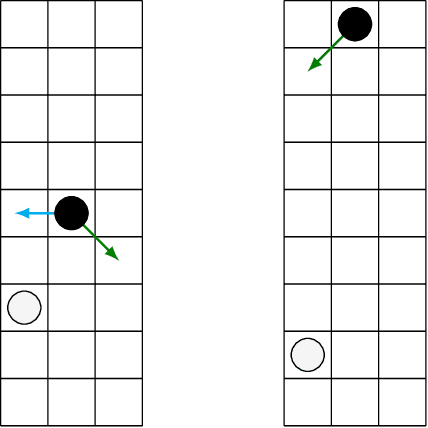
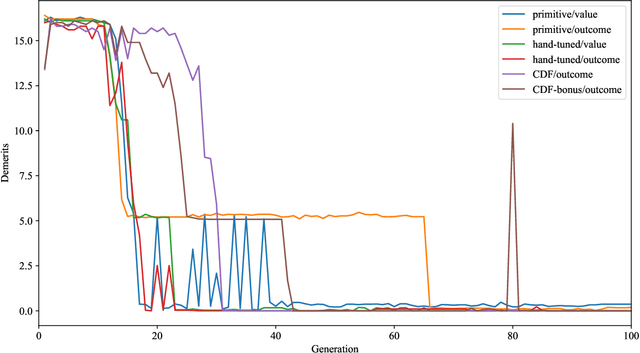
The AlphaZero algorithm for the learning of strategy games via self-play, which has produced superhuman ability in the games of Go, chess, and shogi, uses a quantitative reward function for game outcomes, requiring the users of the algorithm to explicitly balance different components of the reward against each other, such as the game winner and margin of victory. We present a modification to the AlphaZero algorithm that requires only a total ordering over game outcomes, obviating the need to perform any quantitative balancing of reward components. We demonstrate that this system learns optimal play in a comparable amount of time to AlphaZero on a sample game.

Noisier2Noise: Learning to Denoise from Unpaired Noisy Data

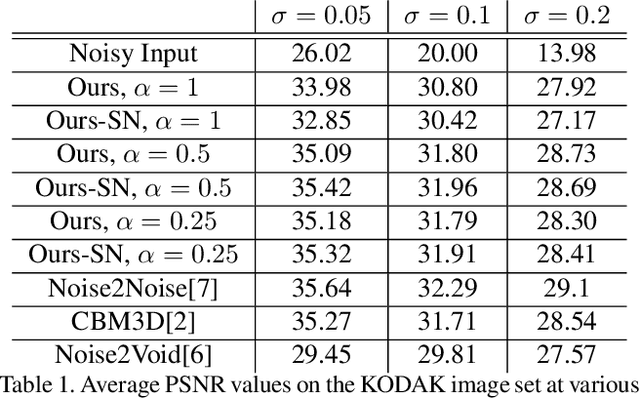
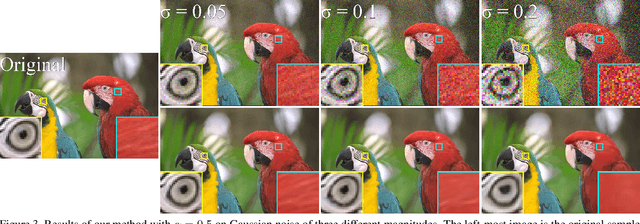
We present a method for training a neural network to perform image denoising without access to clean training examples or access to paired noisy training examples. Our method requires only a single noisy realization of each training example and a statistical model of the noise distribution, and is applicable to a wide variety of noise models, including spatially structured noise. Our model produces results which are competitive with other learned methods which require richer training data, and outperforms traditional non-learned denoising methods. We present derivations of our method for arbitrary additive noise, an improvement specific to Gaussian additive noise, and an extension to multiplicative Bernoulli noise.

Monotone Learning with Rectified Wire Networks

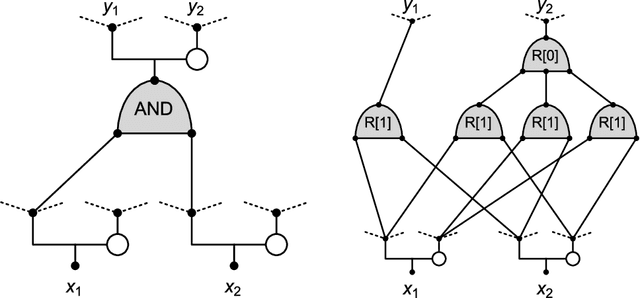
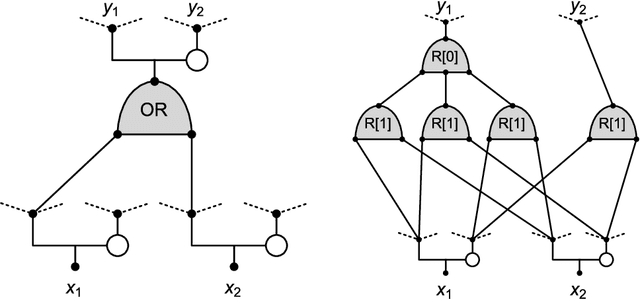
We introduce a new neural network model, together with a tractable and monotone online learning algorithm. Our model describes feed-forward networks for classification, with one output node for each class. The only nonlinear operation is rectification using a ReLU function with a bias. However, there is a rectifier on every edge rather than at the nodes of the network. There are also weights, but these are positive, static, and associated with the nodes. Our "rectified wire" networks are able to represent arbitrary Boolean functions. Only the bias parameters, on the edges of the network, are learned. Another departure in our approach, from standard neural networks, is that the loss function is replaced by a constraint. This constraint is simply that the value of the output node associated with the correct class should be zero. Our model has the property that the exact norm-minimizing parameter update, required to correctly classify a training item, is the solution to a quadratic program that can be computed with a few passes through the network. We demonstrate a training algorithm using this update, called sequential deactivation (SDA), on MNIST and some synthetic datasets. Upon adopting a natural choice for the nodal weights, SDA has no hyperparameters other than those describing the network structure. Our experiments explore behavior with respect to network size and depth in a family of sparse expander networks.

Proactive Message Passing on Memory Factor Networks

We introduce a new type of graphical model that we call a "memory factor network" (MFN). We show how to use MFNs to model the structure inherent in many types of data sets. We also introduce an associated message-passing style algorithm called "proactive message passing"' (PMP) that performs inference on MFNs. PMP comes with convergence guarantees and is efficient in comparison to competing algorithms such as variants of belief propagation. We specialize MFNs and PMP to a number of distinct types of data (discrete, continuous, labelled) and inference problems (interpolation, hypothesis testing), provide examples, and discuss approaches for efficient implementation.