A logical word embedding for learning grammar

We introduce the logical grammar emdebbing (LGE), a model inspired by pregroup grammars and categorial grammars to enable unsupervised inference of lexical categories and syntactic rules from a corpus of text. LGE produces comprehensible output summarizing its inferences, has a completely transparent process for producing novel sentences, and can learn from as few as a hundred sentences.

A transparent approach to data representation

We use a binary attribute representation (BAR) model to describe a data set of Netflix viewers' ratings of movies. We classify the viewers with discrete bits rather than continuous parameters, which makes the representation compact and transparent. The attributes are easy to interpret, and we need far fewer attributes than similar methods do to achieve the same level of error. We also take advantage of the nonuniform distribution of ratings among the movies in the data set to train on a small selection of movies without compromising performance on the rest of the movies.

Learning grammar with a divide-and-concur neural network

We implement a divide-and-concur iterative projection approach to context-free grammar inference. Unlike most state-of-the-art models of natural language processing, our method requires a relatively small number of discrete parameters, making the inferred grammar directly interpretable -- one can read off from a solution how to construct grammatically valid sentences. Another advantage of our approach is the ability to infer meaningful grammatical rules from just a few sentences, compared to the hundreds of gigabytes of training data many other models employ. We demonstrate several ways of applying our approach: classifying words and inferring a grammar from scratch, taking an existing grammar and refining its categories and rules, and taking an existing grammar and expanding its lexicon as it encounters new words in new data.

Avoiding Traps in Nonconvex Problems

Iterative projection methods may become trapped at non-solutions when the constraint sets are nonconvex. Two kinds of parameters are available to help avoid this behavior and this study gives examples of both. The first kind of parameter, called a hyperparameter, includes any kind of parameter that appears in the definition of the iteration rule itself. The second kind comprises metric parameters in the definition of the constraint sets, a feature that arises when the problem to be solved has two or more kinds of variables. Through examples we show the importance of properly tuning both kinds of parameters and offer heuristic interpretations of the observed behavior.

Reconstructing cellular automata rules from observations at nonconsecutive times

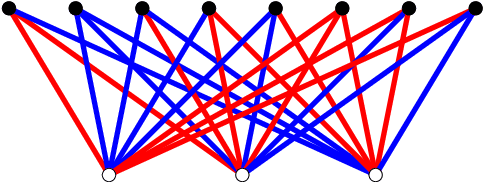
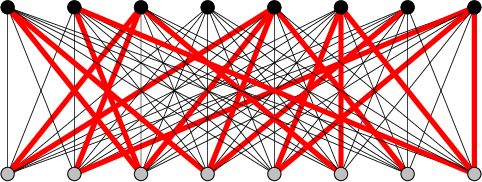
Recent experiments by Springer and Kenyon have shown that a deep neural network can be trained to predict the action of $t$ steps of Conway's Game of Life automaton given millions of examples of this action on random initial states. However, training was never completely successful for $t>1$, and even when successful, a reconstruction of the elementary rule ($t=1$) from $t>1$ data is not within the scope of what the neural network can deliver. We describe an alternative network-like method, based on constraint projections, where this is possible. From a single data item this method perfectly reconstructs not just the automaton rule but also the states in the time steps it did not see. For a unique reconstruction, the size of the initial state need only be large enough that it and the $t-1$ states it evolves into contain all possible automaton input patterns. We demonstrate the method on 1D binary cellular automata that take inputs from $n$ adjacent cells. The unknown rules in our experiments are not restricted to simple rules derived from a few linear functions on the inputs (as in Game of Life), but include all $2^{2^n}$ possible rules on $n$ inputs. Our results extend to $n=6$, for which exhaustive rule-search is not feasible. By relaxing translational symmetry in space and also time, our method is attractive as a platform for the learning of binary data, since the discreteness of the variables does not pose the same challenge it does for gradient-based methods.

Learning Without Loss

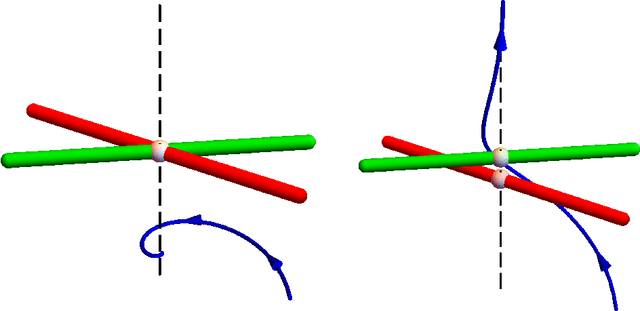
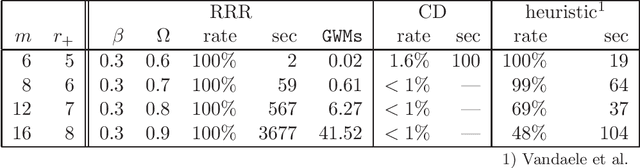
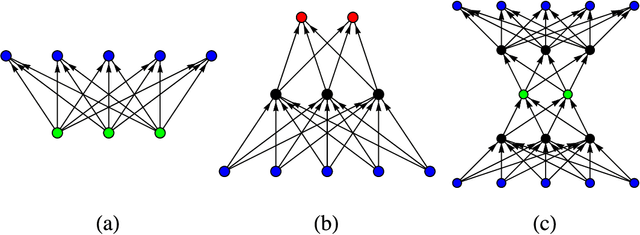
We explore a new approach for training neural networks where all loss functions are replaced by hard constraints. The same approach is very successful in phase retrieval, where signals are reconstructed from magnitude constraints and general characteristics (sparsity, support, etc.). Instead of taking gradient steps, the optimizer in the constraint based approach, called relaxed-reflect-reflect (RRR), derives its steps from projections to local constraints. In neural networks one such projection makes the minimal modification to the inputs $x$, the associated weights $w$, and the pre-activation value $y$ at each neuron, to satisfy the equation $x\cdot w=y$. These projections, along with a host of other local projections (constraining pre- and post-activations, etc.) can be partitioned into two sets such that all the projections in each set can be applied concurrently, across the network and across all data in the training batch. This partitioning into two sets is analogous to the situation in phase retrieval and the setting for which the general purpose RRR optimizer was designed. Owing to the novelty of the method, this paper also serves as a self-contained tutorial. Starting with a single-layer network that performs non-negative matrix factorization, and concluding with a generative model comprising an autoencoder and classifier, all applications and their implementations by projections are described in complete detail. Although the new approach has the potential to extend the scope of neural networks (e.g. by defining activation not through functions but constraint sets), most of the featured models are standard to allow comparison with stochastic gradient descent.

Monotone Learning with Rectified Wire Networks

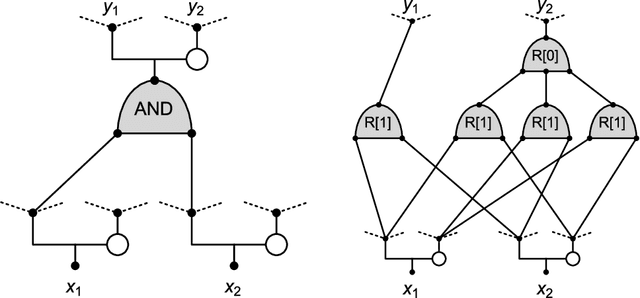
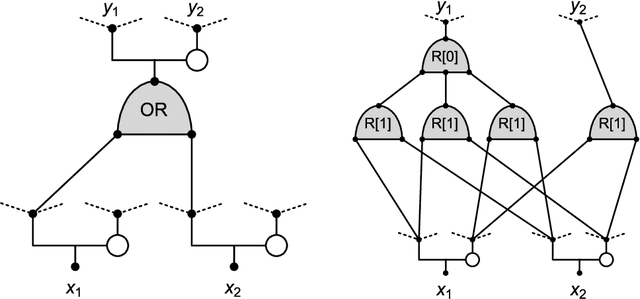
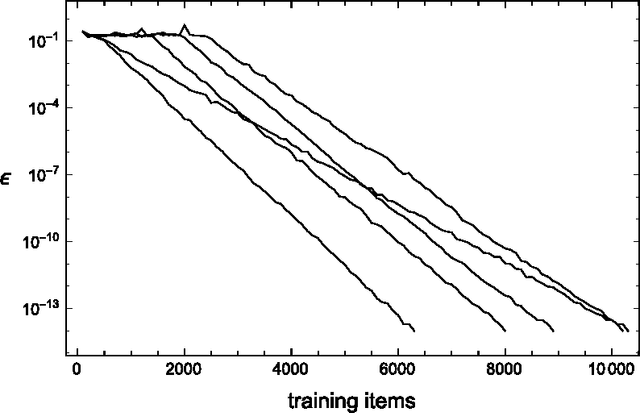
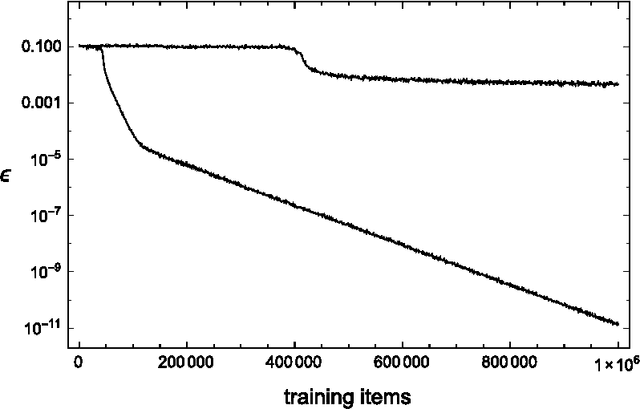
We introduce a new neural network model, together with a tractable and monotone online learning algorithm. Our model describes feed-forward networks for classification, with one output node for each class. The only nonlinear operation is rectification using a ReLU function with a bias. However, there is a rectifier on every edge rather than at the nodes of the network. There are also weights, but these are positive, static, and associated with the nodes. Our "rectified wire" networks are able to represent arbitrary Boolean functions. Only the bias parameters, on the edges of the network, are learned. Another departure in our approach, from standard neural networks, is that the loss function is replaced by a constraint. This constraint is simply that the value of the output node associated with the correct class should be zero. Our model has the property that the exact norm-minimizing parameter update, required to correctly classify a training item, is the solution to a quadratic program that can be computed with a few passes through the network. We demonstrate a training algorithm using this update, called sequential deactivation (SDA), on MNIST and some synthetic datasets. Upon adopting a natural choice for the nodal weights, SDA has no hyperparameters other than those describing the network structure. Our experiments explore behavior with respect to network size and depth in a family of sparse expander networks.

A network that learns Strassen multiplication

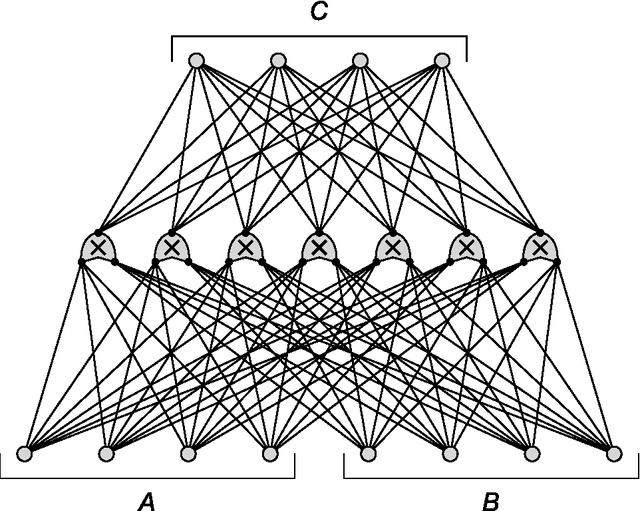
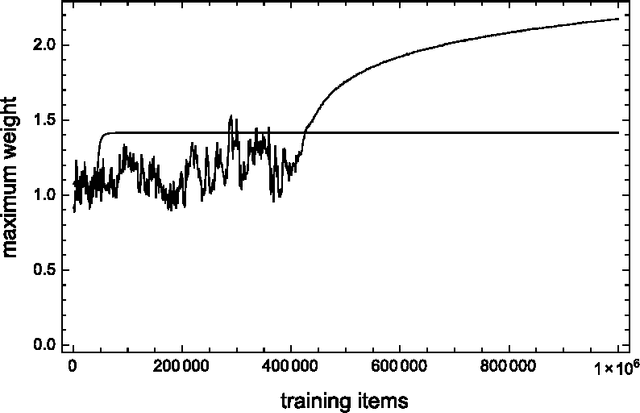
We study neural networks whose only non-linear components are multipliers, to test a new training rule in a context where the precise representation of data is paramount. These networks are challenged to discover the rules of matrix multiplication, given many examples. By limiting the number of multipliers, the network is forced to discover the Strassen multiplication rules. This is the mathematical equivalent of finding low rank decompositions of the $n\times n$ matrix multiplication tensor, $M_n$. We train these networks with the conservative learning rule, which makes minimal changes to the weights so as to give the correct output for each input at the time the input-output pair is received. Conservative learning needs a few thousand examples to find the rank 7 decomposition of $M_2$, and $10^5$ for the rank 23 decomposition of $M_3$ (the lowest known). High precision is critical, especially for $M_3$, to discriminate between true decompositions and "border approximations".

An Improved Three-Weight Message-Passing Algorithm

We describe how the powerful "Divide and Concur" algorithm for constraint satisfaction can be derived as a special case of a message-passing version of the Alternating Direction Method of Multipliers (ADMM) algorithm for convex optimization, and introduce an improved message-passing algorithm based on ADMM/DC by introducing three distinct weights for messages, with "certain" and "no opinion" weights, as well as the standard weight used in ADMM/DC. The "certain" messages allow our improved algorithm to implement constraint propagation as a special case, while the "no opinion" messages speed convergence for some problems by making the algorithm focus only on active constraints. We describe how our three-weight version of ADMM/DC can give greatly improved performance for non-convex problems such as circle packing and solving large Sudoku puzzles, while retaining the exact performance of ADMM for convex problems. We also describe the advantages of our algorithm compared to other message-passing algorithms based upon belief propagation.