Reconstructing cellular automata rules from observations at nonconsecutive times
Paper and Code
Dec 03, 2020
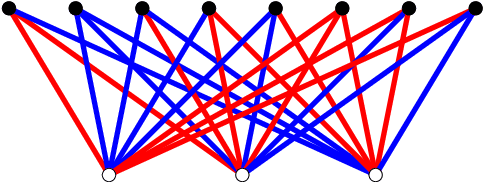
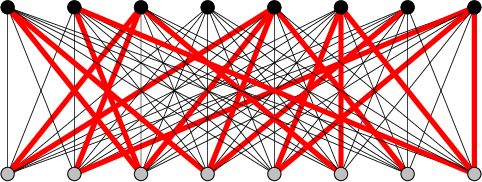

Recent experiments by Springer and Kenyon have shown that a deep neural network can be trained to predict the action of $t$ steps of Conway's Game of Life automaton given millions of examples of this action on random initial states. However, training was never completely successful for $t>1$, and even when successful, a reconstruction of the elementary rule ($t=1$) from $t>1$ data is not within the scope of what the neural network can deliver. We describe an alternative network-like method, based on constraint projections, where this is possible. From a single data item this method perfectly reconstructs not just the automaton rule but also the states in the time steps it did not see. For a unique reconstruction, the size of the initial state need only be large enough that it and the $t-1$ states it evolves into contain all possible automaton input patterns. We demonstrate the method on 1D binary cellular automata that take inputs from $n$ adjacent cells. The unknown rules in our experiments are not restricted to simple rules derived from a few linear functions on the inputs (as in Game of Life), but include all $2^{2^n}$ possible rules on $n$ inputs. Our results extend to $n=6$, for which exhaustive rule-search is not feasible. By relaxing translational symmetry in space and also time, our method is attractive as a platform for the learning of binary data, since the discreteness of the variables does not pose the same challenge it does for gradient-based methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge