Proximal operators for multi-agent path planning

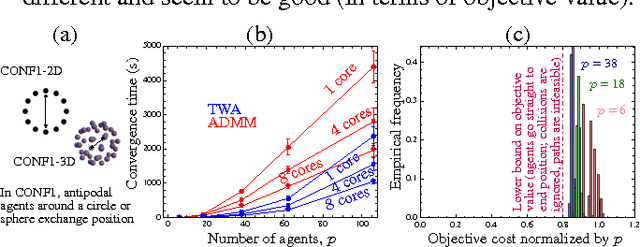
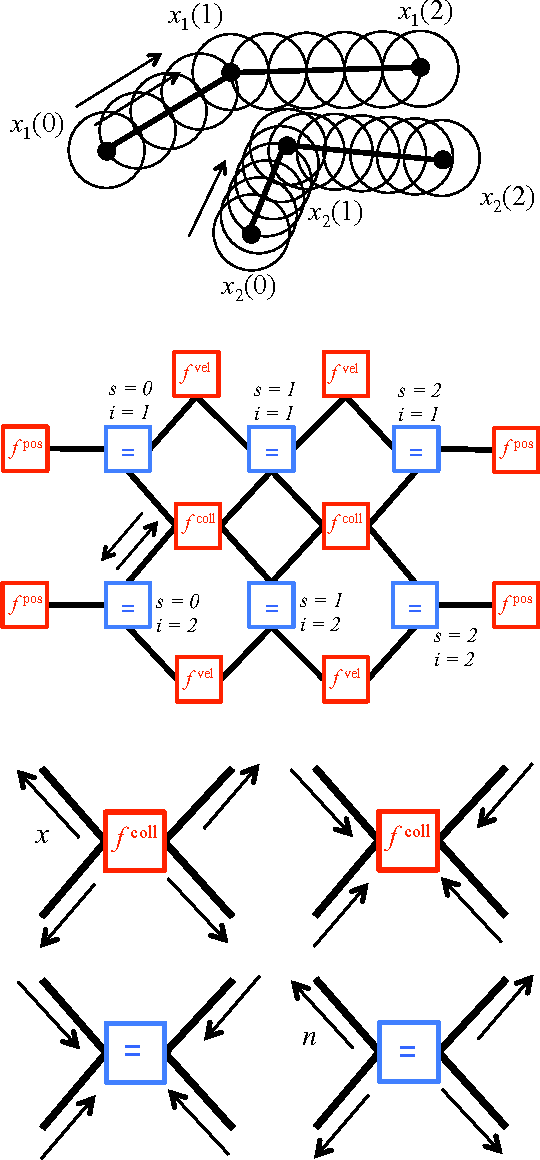
We address the problem of planning collision-free paths for multiple agents using optimization methods known as proximal algorithms. Recently this approach was explored in Bento et al. 2013, which demonstrated its ease of parallelization and decentralization, the speed with which the algorithms generate good quality solutions, and its ability to incorporate different proximal operators, each ensuring that paths satisfy a desired property. Unfortunately, the operators derived only apply to paths in 2D and require that any intermediate waypoints we might want agents to follow be preassigned to specific agents, limiting their range of applicability. In this paper we resolve these limitations. We introduce new operators to deal with agents moving in arbitrary dimensions that are faster to compute than their 2D predecessors and we introduce landmarks, space-time positions that are automatically assigned to the set of agents under different optimality criteria. Finally, we report the performance of the new operators in several numerical experiments.

Methods for Integrating Knowledge with the Three-Weight Optimization Algorithm for Hybrid Cognitive Processing

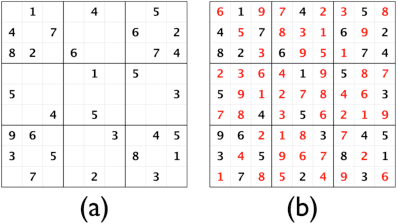
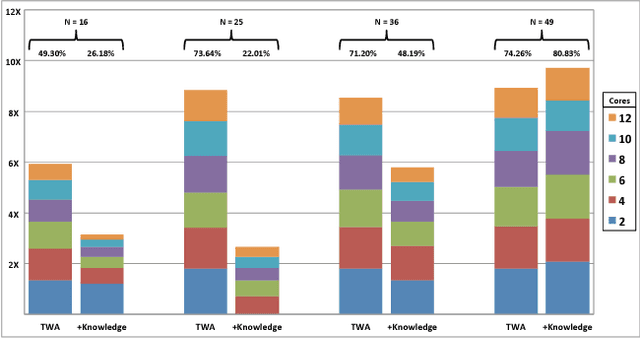
In this paper we consider optimization as an approach for quickly and flexibly developing hybrid cognitive capabilities that are efficient, scalable, and can exploit knowledge to improve solution speed and quality. In this context, we focus on the Three-Weight Algorithm, which aims to solve general optimization problems. We propose novel methods by which to integrate knowledge with this algorithm to improve expressiveness, efficiency, and scaling, and demonstrate these techniques on two example problems (Sudoku and circle packing).

An Improved Three-Weight Message-Passing Algorithm

We describe how the powerful "Divide and Concur" algorithm for constraint satisfaction can be derived as a special case of a message-passing version of the Alternating Direction Method of Multipliers (ADMM) algorithm for convex optimization, and introduce an improved message-passing algorithm based on ADMM/DC by introducing three distinct weights for messages, with "certain" and "no opinion" weights, as well as the standard weight used in ADMM/DC. The "certain" messages allow our improved algorithm to implement constraint propagation as a special case, while the "no opinion" messages speed convergence for some problems by making the algorithm focus only on active constraints. We describe how our three-weight version of ADMM/DC can give greatly improved performance for non-convex problems such as circle packing and solving large Sudoku puzzles, while retaining the exact performance of ADMM for convex problems. We also describe the advantages of our algorithm compared to other message-passing algorithms based upon belief propagation.