Learning Without Loss
Paper and Code
Oct 29, 2019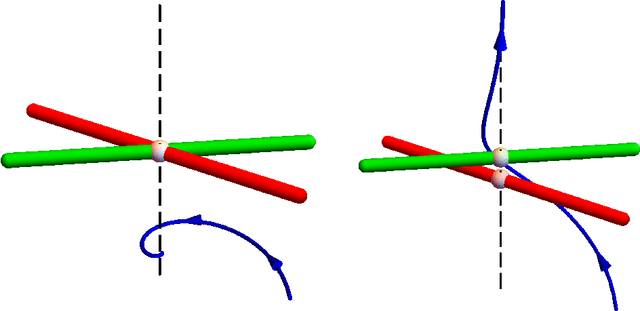
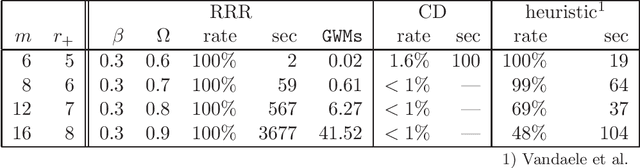
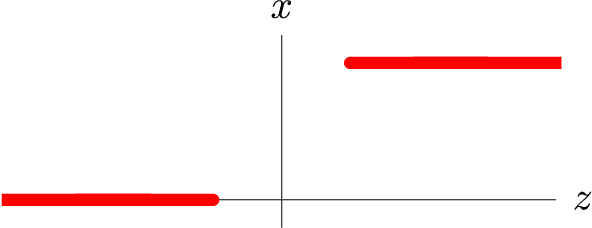
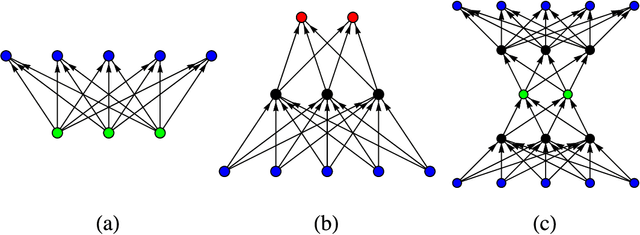
We explore a new approach for training neural networks where all loss functions are replaced by hard constraints. The same approach is very successful in phase retrieval, where signals are reconstructed from magnitude constraints and general characteristics (sparsity, support, etc.). Instead of taking gradient steps, the optimizer in the constraint based approach, called relaxed-reflect-reflect (RRR), derives its steps from projections to local constraints. In neural networks one such projection makes the minimal modification to the inputs $x$, the associated weights $w$, and the pre-activation value $y$ at each neuron, to satisfy the equation $x\cdot w=y$. These projections, along with a host of other local projections (constraining pre- and post-activations, etc.) can be partitioned into two sets such that all the projections in each set can be applied concurrently, across the network and across all data in the training batch. This partitioning into two sets is analogous to the situation in phase retrieval and the setting for which the general purpose RRR optimizer was designed. Owing to the novelty of the method, this paper also serves as a self-contained tutorial. Starting with a single-layer network that performs non-negative matrix factorization, and concluding with a generative model comprising an autoencoder and classifier, all applications and their implementations by projections are described in complete detail. Although the new approach has the potential to extend the scope of neural networks (e.g. by defining activation not through functions but constraint sets), most of the featured models are standard to allow comparison with stochastic gradient descent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge