Surjyendu Ray
Exact inference under the perfect phylogeny model
Aug 22, 2019
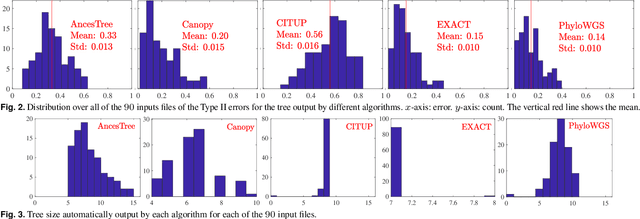
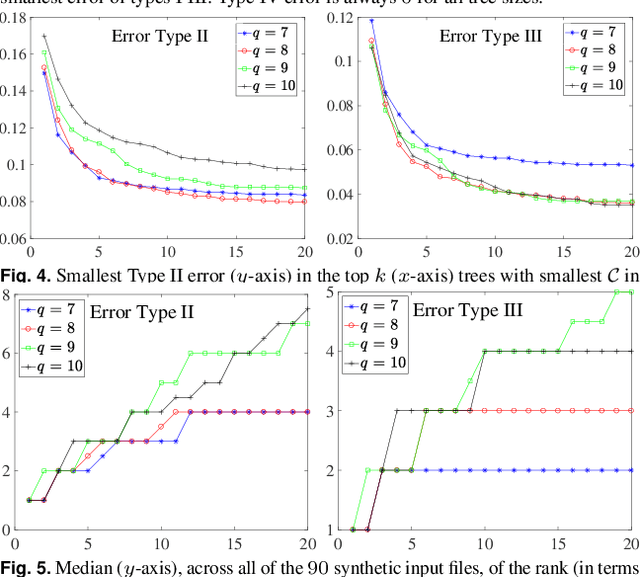
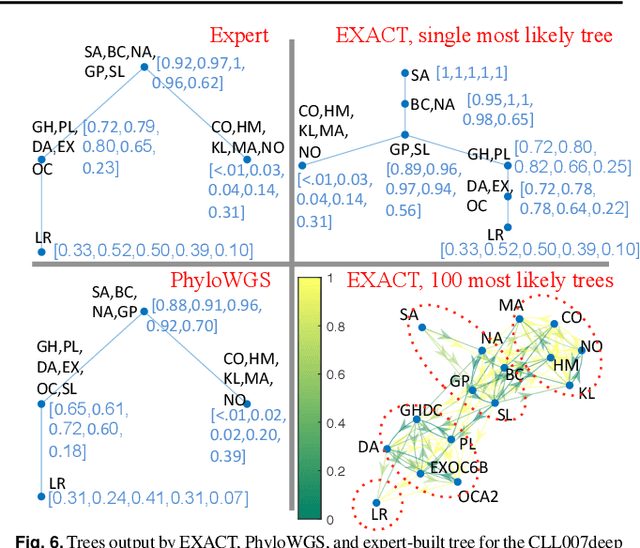
Abstract:Motivation: Many inference tools use the Perfect Phylogeny Model (PPM) to learn trees from noisy variant allele frequency (VAF) data. Learning in this setting is hard, and existing tools use approximate or heuristic algorithms. An algorithmic improvement is important to help disentangle the limitations of the PPM's assumptions from the limitations in our capacity to learn under it. Results: We make such improvement in the scenario, where the mutations that are relevant for evolution can be clustered into a small number of groups, and the trees to be reconstructed have a small number of nodes. We use a careful combination of algorithms, software, and hardware, to develop EXACT: a tool that can explore the space of all possible phylogenetic trees, and performs exact inference under the PPM with noisy data. EXACT allows users to obtain not just the most-likely tree for some input data, but exact statistics about the distribution of trees that might explain the data. We show that EXACT outperforms several existing tools for this same task. Availability: https://github.com/surjray-repos/EXACT
On the Complexity of the Weighted Fused Lasso
Apr 19, 2018


Abstract:The solution path of the 1D fused lasso for an $n$-dimensional input is piecewise linear with $\mathcal{O}(n)$ segments (Hoefling et al. 2010 and Tibshirani et al 2011). However, existing proofs of this bound do not hold for the weighted fused lasso. At the same time, results for the generalized lasso, of which the weighted fused lasso is a special case, allow $\Omega(3^n)$ segments (Mairal et al. 2012). In this paper, we prove that the number of segments in the solution path of the weighted fused lasso is $\mathcal{O}(n^2)$, and that, for some instances, it is $\Omega(n^2)$. We also give a new, very simple, proof of the $\mathcal{O}(n)$ bound for the fused lasso.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge