Tuning Over-Relaxed ADMM
Paper and Code
Mar 05, 2018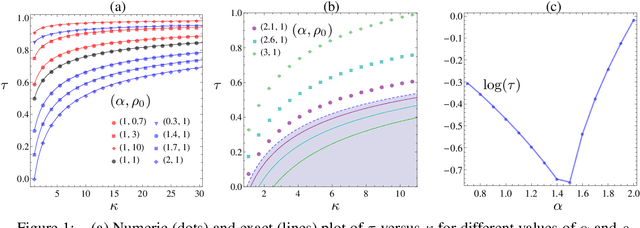
The framework of Integral Quadratic Constraints (IQC) reduces the computation of upper bounds on the convergence rate of several optimization algorithms to a semi-definite program (SDP). In the case of over-relaxed Alternating Direction Method of Multipliers (ADMM), an explicit and closed form solution to this SDP was derived in our recent work [1]. The purpose of this paper is twofold. First, we summarize these results. Second, we explore one of its consequences which allows us to obtain general and simple formulas for optimal parameter selection. These results are valid for arbitrary strongly convex objective functions.
* NIPS 2016, Optimizing the Optimizer Workshop
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge