Distributed Optimization, Averaging via ADMM, and Network Topology
Paper and Code
Sep 05, 2020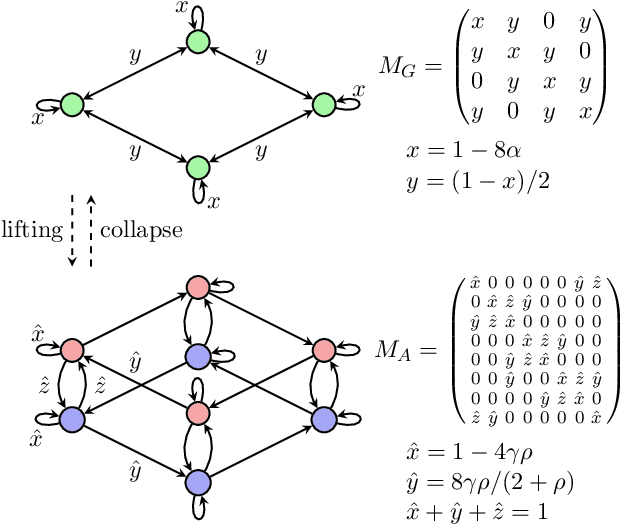
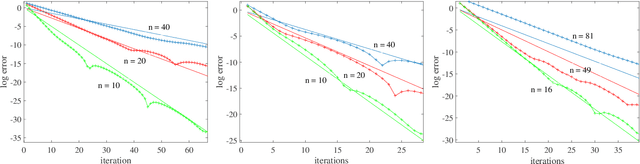
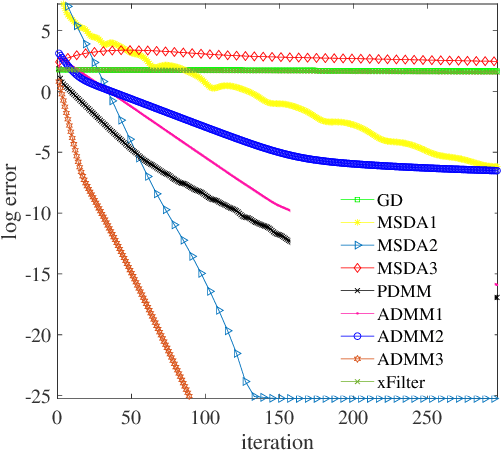
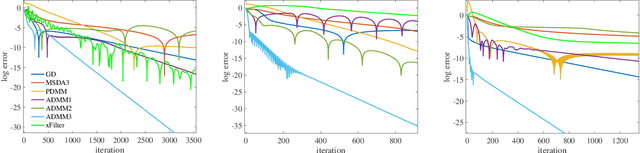
There has been an increasing necessity for scalable optimization methods, especially due to the explosion in the size of datasets and model complexity in modern machine learning applications. Scalable solvers often distribute the computation over a network of processing units. For simple algorithms such as gradient descent the dependency of the convergence time with the topology of this network is well-known. However, for more involved algorithms such as the Alternating Direction Methods of Multipliers (ADMM) much less is known. At the heart of many distributed optimization algorithms there exists a gossip subroutine which averages local information over the network, and whose efficiency is crucial for the overall performance of the method. In this paper we review recent research in this area and, with the goal of isolating such a communication exchange behaviour, we compare different algorithms when applied to a canonical distributed averaging consensus problem. We also show interesting connections between ADMM and lifted Markov chains besides providing an explicitly characterization of its convergence and optimal parameter tuning in terms of spectral properties of the network. Finally, we empirically study the connection between network topology and convergence rates for different algorithms on a real world problem of sensor localization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge