An Explicit Rate Bound for the Over-Relaxed ADMM
Paper and Code
Mar 05, 2018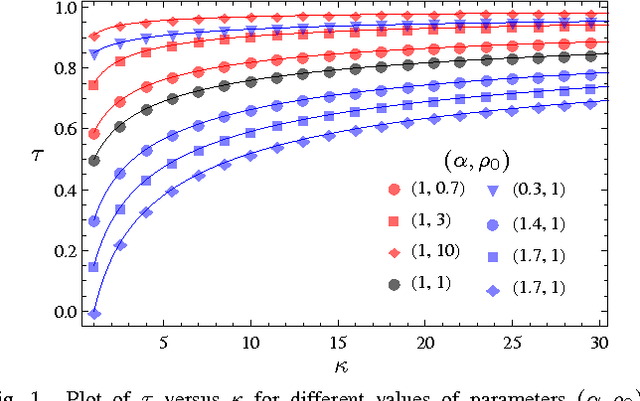
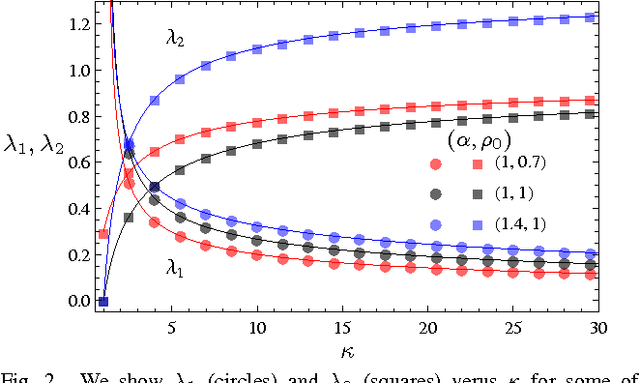
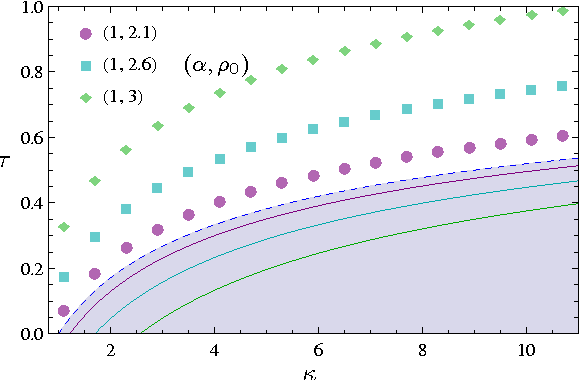
The framework of Integral Quadratic Constraints of Lessard et al. (2014) reduces the computation of upper bounds on the convergence rate of several optimization algorithms to semi-definite programming (SDP). Followup work by Nishihara et al. (2015) applies this technique to the entire family of over-relaxed Alternating Direction Method of Multipliers (ADMM). Unfortunately, they only provide an explicit error bound for sufficiently large values of some of the parameters of the problem, leaving the computation for the general case as a numerical optimization problem. In this paper we provide an exact analytical solution to this SDP and obtain a general and explicit upper bound on the convergence rate of the entire family of over-relaxed ADMM. Furthermore, we demonstrate that it is not possible to extract from this SDP a general bound better than ours. We end with a few numerical illustrations of our result and a comparison between the convergence rate we obtain for the ADMM with known convergence rates for the Gradient Descent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge