Geometric Methods for Sampling, Optimisation, Inference and Adaptive Agents
Paper and Code
Mar 20, 2022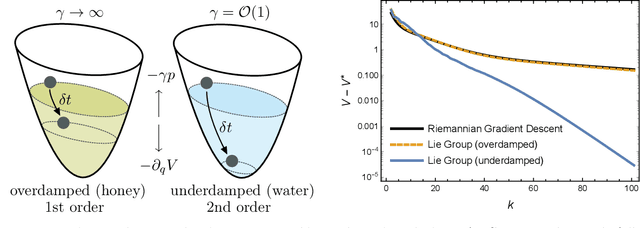
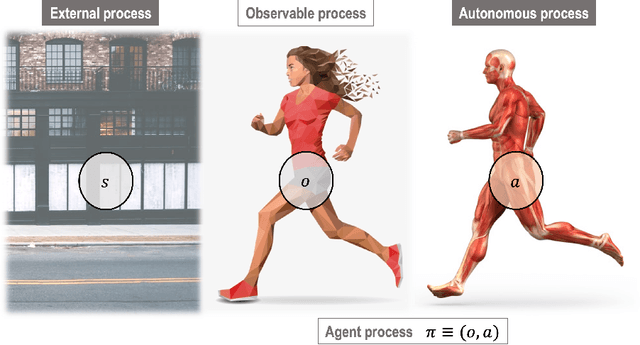
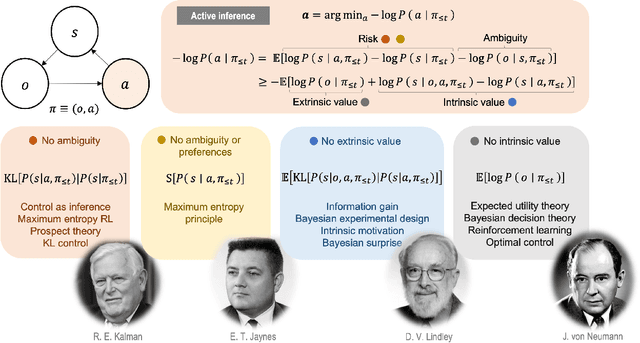
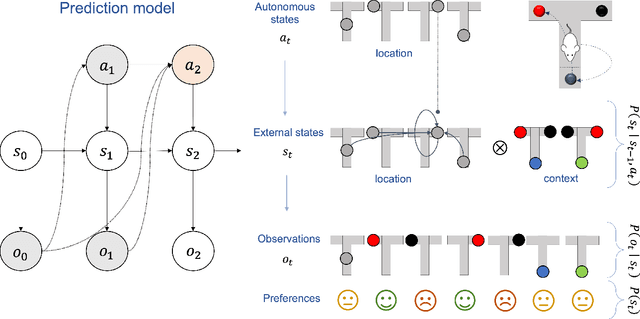
In this chapter, we identify fundamental geometric structures that underlie the problems of sampling, optimisation, inference and adaptive decision-making. Based on this identification, we derive algorithms that exploit these geometric structures to solve these problems efficiently. We show that a wide range of geometric theories emerge naturally in these fields, ranging from measure-preserving processes, information divergences, Poisson geometry, and geometric integration. Specifically, we explain how \emph{(i)} leveraging the symplectic geometry of Hamiltonian systems enable us to construct (accelerated) sampling and optimisation methods, \emph{(ii)} the theory of Hilbertian subspaces and Stein operators provides a general methodology to obtain robust estimators, \emph{(iii)} preserving the information geometry of decision-making yields adaptive agents that perform active inference. Throughout, we emphasise the rich connections between these fields; e.g., inference draws on sampling and optimisation, and adaptive decision-making assesses decisions by inferring their counterfactual consequences. Our exposition provides a conceptual overview of underlying ideas, rather than a technical discussion, which can be found in the references herein.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge