Gradient Flows and Accelerated Proximal Splitting Methods

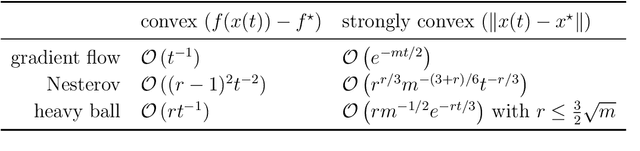
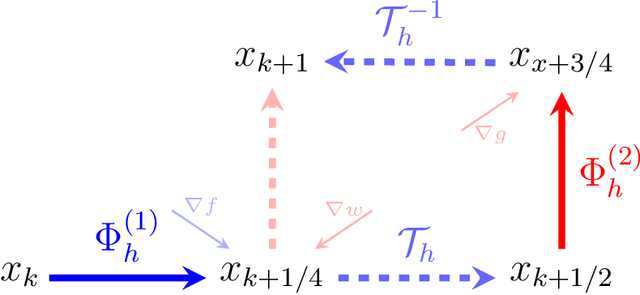
Proximal based algorithms are well-suited to nonsmooth optimization problems with important applications in signal processing, control theory, statistics and machine learning. There are essentially four basic types of proximal algorithms based on fixed-point iteration currently known: forward-backward splitting, forward-backward-forward or Tseng splitting, Douglas-Rachford, and the very recent Davis-Yin three-operator splitting. In addition, the alternating direction method of multipliers (ADMM) is also closely related. In this paper, we show that all these different methods can be derived from the gradient flow by using splitting methods for ordinary differential equations. Furthermore, applying similar discretization scheme to a particular second order differential equation results in accelerated variants of the respective algorithm, which can be of Nesterov or heavy ball type, although we treat both simultaneously. Many of the optimization algorithms we derive are new. For instance, we propose accelerated variants of Davis-Yin and two extensions of ADMM together with their accelerated variants. Interestingly, we show that (accelerated) ADMM corresponds to a rebalanced splitting which is a recent technique designed to preserve steady states of the differential equation. Overall, our results strengthen the connections between optimization and continuous dynamical systems and offer a more unified perspective on accelerated methods.