Anthony Baptista
Deep Learning as Ricci Flow
Apr 22, 2024Abstract:Deep neural networks (DNNs) are powerful tools for approximating the distribution of complex data. It is known that data passing through a trained DNN classifier undergoes a series of geometric and topological simplifications. While some progress has been made toward understanding these transformations in neural networks with smooth activation functions, an understanding in the more general setting of non-smooth activation functions, such as the rectified linear unit (ReLU), which tend to perform better, is required. Here we propose that the geometric transformations performed by DNNs during classification tasks have parallels to those expected under Hamilton's Ricci flow - a tool from differential geometry that evolves a manifold by smoothing its curvature, in order to identify its topology. To illustrate this idea, we present a computational framework to quantify the geometric changes that occur as data passes through successive layers of a DNN, and use this framework to motivate a notion of `global Ricci network flow' that can be used to assess a DNN's ability to disentangle complex data geometries to solve classification problems. By training more than $1,500$ DNN classifiers of different widths and depths on synthetic and real-world data, we show that the strength of global Ricci network flow-like behaviour correlates with accuracy for well-trained DNNs, independently of depth, width and data set. Our findings motivate the use of tools from differential and discrete geometry to the problem of explainability in deep learning.
Zoo Guide to Network Embedding
May 05, 2023Abstract:Networks have provided extremely successful models of data and complex systems. Yet, as combinatorial objects, networks do not have in general intrinsic coordinates and do not typically lie in an ambient space. The process of assigning an embedding space to a network has attracted lots of interest in the past few decades, and has been efficiently applied to fundamental problems in network inference, such as link prediction, node classification, and community detection. In this review, we provide a user-friendly guide to the network embedding literature and current trends in this field which will allow the reader to navigate through the complex landscape of methods and approaches emerging from the vibrant research activity on these subjects.
Universal Multilayer Network Exploration by Random Walk with Restart
Jul 09, 2021
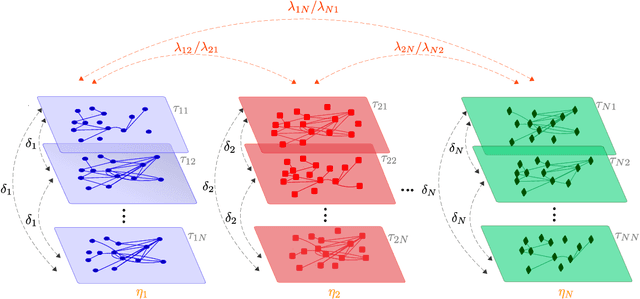

Abstract:The amount and variety of data is increasing drastically for several years. These data are often represented as networks, which are then explored with approaches arising from network theory. Recent years have witnessed the extension of network exploration methods to leverage more complex and richer network frameworks. Random walks, for instance, have been extended to explore multilayer networks. However, current random walk approaches are limited in the combination and heterogeneity of network layers they can handle. New analytical and numerical random walk methods are needed to cope with the increasing diversity and complexity of multilayer networks. We propose here MultiXrank, a Python package that enables Random Walk with Restart (RWR) on any kind of multilayer network with an optimized implementation. This package is supported by a universal mathematical formulation of the RWR. We evaluated MultiXrank with leave-one-out cross-validation and link prediction, and introduced protocols to measure the impact of the addition or removal of multilayer network data on prediction performances. We further measured the sensitivity of MultiXrank to input parameters by in-depth exploration of the parameter space. Finally, we illustrate the versatility of MultiXrank with different use-cases of unsupervised node prioritization and supervised classification in the context of human genetic diseases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge